韋格納分布Wigner Distribution Function(縮寫為WDF),是時頻分析中的一種分析方式,以下為其方程式的轉換:

經整理後得到 
連續訊號要得到其數位實現,必須經過採樣(sampling), 使得 
重新回顧上述式子可以得到,
當  不是 time-limited signal,會很難實現。
不是 time-limited signal,會很難實現。
於是,通常我們會假設  ,也就是
,也就是  為一個有限長度的訊號:
為一個有限長度的訊號:
如圖所示:
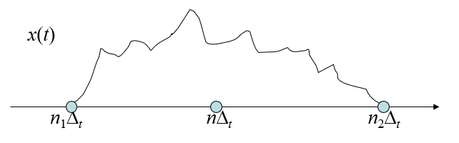
此時 ![{\displaystyle x((n+p)\Delta _{t})x^{*}((n-p)\Delta _{t})=0,\ if\ (n+p)\not \in [n_{1},n_{2}]\ or\ (n-p)\not \in [n1,n2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/828d4f79406d8e8e29ae4a4bc963b7b79d850774)
繼續討論  的範圍 ( 於
的範圍 ( 於 為一固定值時 ):
為一固定值時 ):
- 對於
 :
:
- 對於
 :
: ,也就是
,也就是 
於是便得知  的範圍為:
的範圍為:
用圖片來理解:

注意:當  或
或  時,找不到適當的
時,找不到適當的  來滿足不等式。
來滿足不等式。
整理前述說明後,WDF的數位實現的數學式可整理為:
 ,
,

( 

![{\displaystyle p\in [-Q,Q],\ n\in [n_{1},n_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/764ebfa58d8addc470bb5ec4cee969ec69fe429c) )
)
以下提供3種實現方式:
- 暴力法 (Direct Implementation)
- 離散傅立葉轉換(Using Discrete time Fourier Transform)
- Chirp-Z轉換
暴力法(Direct Implementation)
[编辑]根據  , (
, ( 

![{\displaystyle p\in [-Q,Q],\ n\in [n_{1},n_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/764ebfa58d8addc470bb5ec4cee969ec69fe429c) )
)
令 共有
共有 點,
點, 共有
共有 點,此算法其複雜度為
點,此算法其複雜度為 



當  ,
,
 , 令
, 令 


其中:


此實現方式的複雜度為 


Step1. 
Step2. ![{\displaystyle X_{2}[n,m]=\sum _{p=-Q}^{Q}x_{1}[n,p]c[m-p],\ c[m]=e^{j2\pi m^{2}\Delta _{t}\Delta _{f}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0cc9ac39ab3bde2008b815f70ea998362b8065b)
Step3. ![{\displaystyle X(n\Delta _{t},m\Delta _{f})=2\Delta _{t}e^{-j2\pi m^{2}\Delta _{t}\Delta _{f}}X_{2}[n,m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2a7f743de3e9948d71d3393a79f97021379d2d2)
此實現方式複雜度一樣為  但相較使用離散傅立葉轉換方式而言(
但相較使用離散傅立葉轉換方式而言( ![{\displaystyle [\ \theta (\ T3N\log(N)\ )\ =\ \theta (\ TN\log(N)\ )\ ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57f8ccceb9ea714fac12a3d2b8dc5057b99feeea) 數字3來自於convolution運算 IFT(FT * FT) ),速度來的更快。
數字3來自於convolution運算 IFT(FT * FT) ),速度來的更快。
- Jian-Jiun Ding, Time frequency analysis and wavelet transform class note, the Department of Electrical Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2019.








![{\displaystyle x((n+p)\Delta _{t})x^{*}((n-p)\Delta _{t})=0,\ if\ (n+p)\not \in [n_{1},n_{2}]\ or\ (n-p)\not \in [n1,n2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/828d4f79406d8e8e29ae4a4bc963b7b79d850774)















![{\displaystyle p\in [-Q,Q],\ n\in [n_{1},n_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/764ebfa58d8addc470bb5ec4cee969ec69fe429c)


















![{\displaystyle X_{2}[n,m]=\sum _{p=-Q}^{Q}x_{1}[n,p]c[m-p],\ c[m]=e^{j2\pi m^{2}\Delta _{t}\Delta _{f}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0cc9ac39ab3bde2008b815f70ea998362b8065b)
![{\displaystyle X(n\Delta _{t},m\Delta _{f})=2\Delta _{t}e^{-j2\pi m^{2}\Delta _{t}\Delta _{f}}X_{2}[n,m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2a7f743de3e9948d71d3393a79f97021379d2d2)

![{\displaystyle [\ \theta (\ T3N\log(N)\ )\ =\ \theta (\ TN\log(N)\ )\ ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57f8ccceb9ea714fac12a3d2b8dc5057b99feeea)