相对论时空

为什么想做这一个题目

因为一部电影星际效应，里面主角要去寻找另一个适合人类生存的星球，有些星球位于邻近黑洞的地方，他们越靠近，到达那个星球，他们时间就会变得越慢。他们自身并没有发觉时间变慢，他们在那个星球上待几个小时，但是相对的在远方等著他们回来的伙伴却已经历经好几十年的岁月了。而当他再回去找到他女儿时，他女儿竟然已经变成比他还老的奶奶了！

因为这个问题所以我开始想了解这是为什么？渐渐的就去了解到相对论。

相对论的两个基本假设

• 光速不变原理。

科学家测光沿著地球转向的速度，以及光逆著地球转向的速度，按古典的观念来说，沿著地球转向时原本的光速加上地球转速测得的值应该会比光速要快，而逆著地球转向测得的值会比光速小，但实验结果却是两边光速都一模一样。

• 相对性原理

我们无法真的知道每个座标系谁是静止谁是运动中的。也就是说物理定律在一切参考系中都具有相同的形式。

劳伦兹变换

在两个等速直线相对运动的座标系(惯性座标系)，维持光速在各座标皆相同所需要的时空变换。

时间膨胀

等速运动的物体带在身上的时钟，用静系观察者的时钟去测量，不论运动方向，测量结果“动钟”都随著运动速度增加而变慢。

• 光速运动的物体(如光子)，它的时间是静止的。
• 速度低于光速的物体，其时间膨胀的程度遵循洛仑兹变换：$\Delta t={\frac {\Delta t_{0}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$

长度收缩

对某运动物体进行观测，在运动的那个方向，长度会比相对于物体静止的观测者观测到的同一长度要短。

$\Delta L=\Delta L_{0}{\sqrt {1-\left({\frac {v}{c}}\right)^{2}}}$

相对论质量

$m={\frac {m_{0}}{\sqrt {1-\left({\frac {v}{c}}\right)^{2}}}}$

m₀指绝对质量(及牛顿力学中的质量)，m为相对论质量。

由公式可以看出：

1. 对于一个有质量的物体，其速度v不可能等于或者超过光速，否则分母将会无意义或为一个虚数(注：光子没有质量，因此其速度可以达到光速)。
2. 当某有质量之物体移动速率越接近光速，相对论质量会变重。
3. 当v远小于c时，m近似于m₀，符合牛顿力学定律。

解释时间膨胀

甲观察者在车厢内时

图一

• 当甲观察者在内部时，光源从A点射出，到达B点为一秒30万公里，并折回来，总共是两秒。
• 甲会观察到光线是直线来回。

乙观察者在车厢外时

图二

• 当乙观察者站在车厢外，车由左至右行驶，乙会看到光线往右上方射出，再往右下折返，形成一个三角形的轨迹。
• 图二的A点跟B点距离变长，但是根据相对论光速还是必须以每秒三十万公里速度前进，所以必须要时间膨胀，才能使的光速都保持在每秒三十万公里的速度前进。

计算

只有透过劳伦兹变换公式的时间膨胀效应，才可以使光速在不同的惯性座标系之下，都还是维持每秒三十万公里。

假设车厢高度 30 万公里，车厢以${\frac {2}{3}}$光速相对月台前进。甲观察者在车厢内，看到光自车厢底射向车厢顶历时一秒，从车箱顶再反射回车厢底又历时一秒(如图一)，光速恰为每秒 30 万公里。

现在乙观察在月台上，看到光的轨迹如图二，依下列步骤进行计算，验证乙观察者测得的光速。

1. 时间由1秒膨胀到1.34秒：${\frac {1}{\sqrt {1-({\frac {{\frac {2}{3}}c}{c}})^{2}}}}={\frac {1}{\sqrt {1-{\frac {4}{9}}}}}={\frac {1}{\sqrt {\frac {5}{9}}}}={\frac {1}{0.745}}=1.34$
2. 每秒20万公里为${\frac {2}{3}}$光速，时间膨胀到1.34秒后，车厢前进 ${\overline {AA'}}$ 为26.8万公里 ：$20*1.34=26.8$(万)
3. 斜边 ${\overline {AB}}$ 的平方为 $26.8^{2}+30^{2}=1618.24$(万万)
4. 时间膨胀到1.34秒，光走了斜边 ${\overline {AB}}$ 40.227万公里：${\sqrt {1618.24}}=40.227$
5. 月台观察到光轨迹的速度=距离/时间，光速还是接近于30万公里：$40.227/1.34=30.02$

再将车厢与月台的相对速度推广到任意速度

推广到任意速度$v$。

1. 时间由1秒膨胀为${\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$秒$={\sqrt {\frac {c^{2}}{c^{2}-v^{2}}}}$秒
2. ${\overline {AA'}}=v*{\sqrt {\frac {c^{2}}{c^{2}-v^{2}}}}$
3. 斜边${\overline {AB}}^{2}=v^{2}*{\frac {c^{2}}{c^{2}-v^{2}}}+c^{2}=c^{2}({\frac {v^{2}}{c^{2}-v^{2}}}+1)=c^{2}({\frac {v^{2}+c^{2}-v^{2}}{c^{2}-v^{2}}})=c^{2}({\frac {c^{2}}{c^{2}-v^{2}}})$
4. 斜边${\overline {AB}}=c*{\sqrt {\frac {c^{2}}{c^{2}-v^{2}}}}$
5. 光速=斜边/经过时间=${\frac {c{\sqrt {\frac {c^{2}}{c^{2}-v^{2}}}}}{\sqrt {\frac {c^{2}}{c^{2}-v^{2}}}}}=c$

长度收缩

• 高速下的时空
• 当一个物体以接近光速运动时，延运动方向的长度会比相对于物体静止状态观测者观察到的还短。

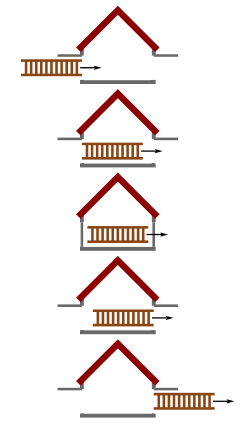
以“谷仓-竿吊诡”(房子-梯子)解释长度收缩

• 假设有一个静止不动的谷仓，前门打开，后门关闭，谷仓总长3公尺。有一个超人类带著一根长3.1公尺的木棍以光速冲向谷仓。当超人类经过谷仓的时候，以古典的观念木棍会有超过谷仓的部份，但是因为超人类是以光速前进，谷仓是静止的，所以木棍因为长度收缩效应变短了，观察者会看到木棍有一段时间是可以完全在谷仓内部。

梯子与房子都静止时

观察者在房中，看到房子静止，梯子因运动而缩短

观察者与梯子同步，看到的是房子缩短而梯子未缩短

• 

  “动”梯通过“静”房示意图

“动”房通过“静”梯示意图

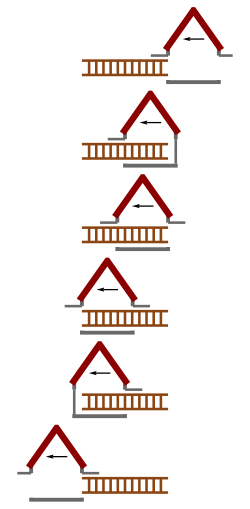
• 此案例中包含两个事件：甲事件是梯子前端到达房子后门，乙事件是梯子尾端到达房子前门。
  1. 梯子长度的定义是：在选定的座标系中，同时量取头尾、两点座标，所得的座标差，即其长度。
  2. 在房子静止的例子中，甲、乙事件是同时的，我们同时量取甲乙事件的座标差，因运动中的长度收缩，运动梯子的长度会小于静止梯子的长度，所以可以挤进房子里。而在梯子挤进房子时，同时关上房子的前后门，然后瞬间再打开前后门，让梯子穿出房子。
  3. 在房子运动的例子中，房子的宽度也缩短了，但甲、乙事件不同，持梯的人看到的是梯子前端“先”到达房子后门(第三格)，然“后”才发生梯子尾端到达房子前门(第四格)。
  4. 一般人会发生错觉而难解，是因为认为“甲、乙事件如果在一个座标系中同时，也会在其他座标系中同时”。但在相对论中没这回事。
• 关闭右侧门竿的长度收缩图示

上面连结所示图中的右侧的门是关著的。长棍因为高速运动已经长度缩短了，当棍子的前端接触到关闭的门，无法再前进时，棍子前端就必须传送讯息通知后端不能继续前进，但前端发送讯息至后端也要一段时间，在那段时间后端依然还在继续前进。

相对论质量

在狭义相对论中，质量并不守恒，而是“质能守恒”，所以相对论质量必须定义成一个依速度而变化的量。

这个动态质量的定义，不能有“每输入一单位能量就能提高固定速度”的特性，否则一定会将质点加速超过光速，应该要有“质点速度越大，每输入一单位能量所得到的速度增加越小，且无法加速到超过光速”的特性。

将相对论质量定义为：$m={\frac {m_{0}}{\sqrt {1-\left({\frac {v}{c}}\right)^{2}}}}$

1. 当 v 为 0 时，m=m₀为静止质量。
2. 这个质量定义会导出 $E=mc^{2}$ ，而此推论也已在实验中多次获得验证了。

推导过程

定义：

1. 速度 $v={\frac {dx}{dt}}$
2. 动量 $P=m*v$
3. 力 $F={\frac {dP}{dt}}$
4. 动能 $dE_{k}=F{dx}$
5. $m={\frac {m_{0}}{\sqrt {1-\left({\frac {v}{c}}\right)^{2}}}}$

(一)由定义 1,2,3,4 得出动能差为 d(m*v)*v

1. $dE_{k}=F{dx}={\frac {dP}{dt}}{dx}$，因为 $F={\frac {dP}{dt}}$
2. $dE_{k}={\frac {d(m*v)}{dt}}{dx}$，因为 $P=m*v$
3. $dE_{k}=d(m*v)*v$，因为 $v={\frac {dx}{dt}}$

(二)得出动能差为 $dm*v^{2}+mvdv$

由上一段得$dE_{k}=(dm*v+m*dv)*v=dm*v^{2}+mvdv$ 第①式

(三)用相对论质量定义得 $dm*v^{2}+mvdv=dm*c^{2}$

关键在相对论质量定义等价于 $dm*c^{2}=dm*v^{2}+mvdv$，请看推导过程如下 1~7 ：

1. 由 定义5 得 $m^{2}c^{2}-m^{2}v^{2}=m_{0}^{2}c^{2}$
2. 两边都对 t 微分，由于 $m_{0}$ 和 $c$ 都不会随时间变化，对时间微分会得 0 ，所以 ${\frac {d(m^{2}*c^{2}-m^{2}*v^{2})}{dt}}=0$
3. ${\frac {d(m^{2}*c^{2})}{dt}}={\frac {d(m^{2}*v^{2})}{dt}}$，化简得 $d(m^{2}*c^{2})=d(m^{2}*v^{2})$
4. c 为常数，m、v均为变数，化简上式得 $d(m^{2})*c^{2}=d(m^{2})*v^{2}+m^{2}*d(v^{2})$
5. 用积分公式得 ${\frac {dm^{2}}{dm}}*dm*c^{2}={\frac {dm^{2}}{dm}}*dm*v^{2}+m^{2}*{\frac {d(v^{2})}{dv}}*dv$
6. 化简上式得 $2m*dm*c^{2}=2m*dm*v^{2}+m^{2}*2v*dv$
7. 三项同除以 2m 得 $dm*c^{2}=dm*v^{2}+mvdv$
8. 代入第①式得：$dE_{k}=dm*v^{2}+mvdv=dm*c^{2}$
9. 对其积分得相对论动能 $E_{k}={\int _{m_{0}}^{m}c^{2}\,dm}=mc^{2}-m_{0}c^{2}$

渺子衰变

渺子寿命：$2.2*10^{-6}$秒，从渺子诞生到衰变的平均运动距离是660公尺

渺子在海平面15公里上空由宇宙线撞击大气分子而形成，照说$2.2*10^{-6}$秒的生命只能走完660公尺。为什么从地面却可以测量到许多渺子？原因是渺子以接近光速的速度运动，所以渺子的时间会变慢，这是时间膨胀。因此从地面上的观察者来看，渺子的寿命比2.2微秒还要长很多，足够时间穿过15公里的大气层到地面。

如果以渺子的角度来观察的话，渺子是静止不动的，反而是地球以光速朝渺子奔来，根据上面讲的长度收缩，地球与渺子之间的距离缩短很多，所以渺子能在衰变之前就到达地面。

渺子的速度是0.9994光速。

1. 时间由1秒膨胀到28.571秒：${\frac {1}{\sqrt {1-({\frac {0.9994c}{c}})^{2}}}}={\frac {1}{\sqrt {1-0.99880036}}}={\frac {1}{\sqrt {0.00119964}}}={\frac {1}{0.035}}=28.571$
2. 0.9994光速为每秒29.982公里，时间膨胀到28.571秒$29.982*28.571=856.616$(万)
3. $856.616^{2}+30^{2}=857.141^{2}$(万万)
4. 光速还是接近于30万公里：$857.141/28.571=30.02$

时间弯曲

时空弯曲

• 有质量的物体都会形成重力场，质量越大，重力场越大。
• 爱因斯坦在1911年发表的广义相对论，所讲的就是重力(万有引力)的本质是物体的分布弯曲了时空，所以宇宙中星体就会造成附近空间的弯曲，邻近的物体接近就会陷进时空弯曲的范围中，形成椭圆的轨道绕著那个星球，速度很慢的物体就会直接撞上去。
• 当物体以高速前进时，进入到时空弯曲范围，他的行径路线就会偏离。例如光，遥远星球发出的光经过许多星球时值线轨道就会偏离，偏离的光只有极少数角度才会被我们观测到。
• 太阳的质量让整个太阳系时空弯曲，所以地球也以椭圆轨道绕著太阳运行。