生物信息学/bwa

软件介绍

新的DNA测序技术产生了大量的短read，需要开发快速准确的read比对程序。MAQ是一种基于哈希表的方法，用于从单个个体比对短read，但对于频繁出现插入缺失的较长read和数百个个体的比对不合适。为了解决这些限制，开发了Burrows-Wheeler Alignment工具（BWA），它可以有效地将短测序read与大型参考序列（例如人类基因组）进行比对，允许不匹配（misMactch）和间隙（gap）。BWA支持基于碱基空间的read，例如Illumina测序机器和来自AB SOLiD机器的颜色空间read。模拟和真实数据的评估表明，BWA比MAQ快约10-20倍，同时实现相似的准确性。此外，BWA输出新的标准SAM（Sequence Alignment/Map）格式的比对。在比对之后进行变异分析和其他下游分析可以使用开源的SAMtools软件包。

软件网址：http://maq.sourceforge.net。

对参考基因组进行短读比对方面已经发展了很多算法，但是对于长读（>200 bp）的比对，现有的算法大多针对低测序错误率的短读进行调整，不适用或者效率不高。因此，需要设计一种能够高效比对长序列的算法。作者基于Burrows-Wheeler算法提出了一种新算法，称为Burrows-Wheeler Aligner's Smith-Waterman Alignment（BWA-SW），能够使用少量内存对长达1 Mb的序列进行比对。结果显示，该算法比BLAT更加准确，与SSAHA2的准确率相当，并且比两者都快几十倍。BWA-SW的源代码已公开。

bwa-sw软件网站：http://bio-bwa.sourceforge.net/

软件发表时的文章：

使用方法

本页面主要介绍BWA的原理，关于使用请参考BWA的使用。

背景介绍

bwa软件开发的背景

将Illumina/Solexa测序技术产生的短read序列比对到大型基因组的比对软件，分为三个类别：基于哈希的比对程序、基于基因组的比对程序和基于字符串合并排序的比对程序。最近，使用Burrows-Wheeler Transform（BWT）的字符串匹配理论引起了几个研究小组的关注，这导致了SOAPv2(http://soap.genomics.org.cn/)、Bowtie(Langmead et al., 2009)和BWA等比对软件的开发。BWA是一种新的比对程序，使用BWT和反向搜索（Ferragina 和 Manzini，2000 年；Lippert，2005 年）来进行精确和近似匹配，具有相对较小的内存占用（Lam 等人，2008 年），能够快速且准确地将短read序列比对到大型基因组。BWA比对软件被证明在模拟和真实数据上的表现优于其他比对程序，特别是在内存使用方面。

基于哈希的比对程序：Eland (Cox, 2007, unpublished material)、RMAP (Smith et al., 2008)、MAQ (Li et al., 2008a)、ZOOM (Lin et al., 2008)、SeqMap (Jiang and Wong, 2008)、CloudBurst (Schatz, 2009) 和 SHRiMP (http://compbio.cs.toronto.edu/shrimp)
基于基因组的比对程序：SOAPv1 (Li et al., 2008b)、PASS (Campagna et al., 2009)、MOM (Eaves and Gao, 2009)、ProbeMatch (Jung Kim et al., 2009)、NovoAlign (http://www.novocraft.com)、ReSEQ (http://code.google.com/p/re-seq)、Mosaik (http://bioinformatics.bc.edu/marthlab/Mosaik) 和 BFAST (http://genome.ucla.edu/bfast)
基于字符串合并排序：Malhis 等人，2009 年

BWA-SW算法

随着 1990 年左右的局部比对软件的发展，例如 FASTA（Pearson 和 Lipman，1988）和 BLAST（Altschul 等，1997），自 2000 年以来开发了新一代更快的 DNA 序列匹配方法，包括 MegaBLAST (Morgulis et al., 2008; Zhang et al., 2000)、SSAHA2 (Ning et al., 2001)、BLAT (Kent, 2002) 和 PatternHunter (Ma et al., 2002)，大大加快了匹配测序read针对大型参考基因组。当新的测序技术出现并产生数百万个短read（<100 bp）时，各种新算法被开发出来，速度提高了 10-1000 倍，包括 SOAP (Li,R. et al., 2008)、MAQ (Li, H. et al., 2008)、 Bowtie（Langmead 等人，2009 年）和 BWA（Li 和 Durbin，2009 年）。然而，Roche/454 测序技术已经开始产生了 >400 bp 的read读数，Illumina 逐渐增加了 >100 bp 的read读数，而 Pacific Bioscience 在早期测试中产生了 1000 bp 的读数（Eid 等，2009）。来自新测序技术的read不再是短的序列，这有效地排除了许多专为不超过 100 bp 的read设计的比对软件。

随着产生长read读数的新测序技术的出现，现有的短read读数比对算法对于长read读数比对来说并不高效。长read比对的目的是寻找局部匹配，因为长read更容易受到结构变异和参考基因组序列中错配组装的影响，但受靠近read末端的错配影响较小。此外，由于长read中更频繁地出现插入和缺失，所以长读数比对算法必须对比对缺口gap持宽容态度。

BWA-SW是一种新的长read排列算法，在两个FM-indices之间使用动态编程来寻找种子，并在它们在参考序列中很少出现的情况下进行扩展。该算法旨在减少高度重复序列的不必要的扩展，从而提高速度。

BWA原理方法

前缀树和字符串匹配

图1：字符串“GOOGOL”的前缀树。符号^标记字符串的开始。节点中的两个数字给出了该节点表示的字符串的 SA 区间（参见第 2.3.3 节）。虚线显示了暴力搜索查询字符串“LOL”的路径，最多允许一个不匹配。正方形中的边缘标签标记了搜索中与查询的不匹配。唯一的命中是粗体节点 [1, 1]，它代表字符串“GOL”。

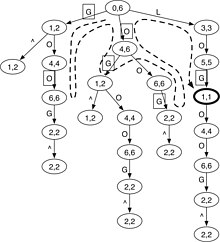
字符串 X 的前缀树是一棵树，其中每条边都用一个符号标记，从叶子到根的路径上边符号的字符串连接给出了唯一的前缀 X。在前缀树上，字符串连接从节点到根的边符号给出了 X 的唯一子串，称为节点所代表的串。请注意，X 的前缀树与 X 的反向后缀树相同，因此后缀树理论也可以应用于前缀树。

使用前缀 trie，测试查询 W 是否是 X 的精确子串相当于找到表示 W 的节点，这可以通过将 W 中的每个符号与一条边匹配，在 O(|W|) 时间内完成，从根。为了允许不匹配，可以彻底遍历特里树并将 W 匹配到每个可能的路径。稍后将展示如何通过使用 W 的前缀信息来加速此搜索。图1给出了“GOOGOL”的前缀树的示例。每个节点中的后缀数组（SA）间隔在第 2.3.3 节中解释。

Burrows–Wheeler转换

图2：为 X=googol$ 构造后缀数组和 BWT 字符串。字符串 X 循环生成 7 个字符串，然后按字典序排序。排序后，第一个符号的位置形成后缀数组（6, 3, 0, 5, 2, 4, 1）并且循环字符串的最后一个符号的串联给出了BWT字符串lo$oogg。

设 Σ 是一个字母表。符号 $ 不存在于 Σ 中，并且按字典顺序小于 Σ 中的所有符号。字符串 X=a0a1…an−1 总是以符号 $ 结尾（即 an−1=$），并且这个符号只出现在末尾。设 X[i]=ai, i=0, 1,..., n−1, 是 X 的第 i 个符号，X[i, j]=ai ...aj 是一个子串，Xi=X[i, n− 1] X 的后缀。X 的后缀数组 S 是整数 0…n−1 的排列，使得 S(i) 是第 i 个最小后缀的起始位置。 X 的 BWT 在 S(i)=0 时定义为 B[i]=$，否则定义为 B[i]=X[S(i)-1]。还将字符串 X 的长度定义为 |X| 因此 |X|=|B|=n。图2 给出了如何构造 BWT 和后缀数组的示例。

图 2 所示的算法在时间和空间上是二次的。然而，这不是必需的。在实践中，通常先构造后缀数组，然后生成 BWT。大多数构建后缀数组的算法至少需要 n⌈log2n⌉ 位的工作空间，对于人类基因组来说，这相当于 12 GB。最近，Hon 等人。 (2007) 给出了一种新算法，该算法使用 n 位工作空间，并且在构建人类基因组 BWT 的高峰时间只需要 <1 GB 内存。该算法在 BWT-SW 中实现（Lam 等人，2008 年）。修改了源代码以使其与 BWA 一起使用。

后缀数组间隔和序列比对

如果字符串 W 是 X 的子字符串，则 X 中 W 每次出现的位置将出现在后缀数组中的一个区间内。这是因为所有以 W 作为前缀的后缀都排序在一起。基于这一观察，定义：

${\underline {R}}(W)=min\left\{k:W\ is\ the\ prefix\ of\ X_{S(k)}\right\}$ (1)

${\overline {R}}(W)=max\left\{k:W\ is\ the\ prefix\ of\ X_{S(k)}\right\}$ (2)

特别是，如果 W 是空字符串，则 R(W)=1 和 ${\textstyle {\overline {R}}=n-1}$ 。

${\textstyle [{\underline {R}}(W),{\overline {R}}(W)]}$ 称为 W 的 SA 区间，X 中所有出现 W 的位置集合是 ${\textstyle \left\{S(k):{\underline {R}}(W)\leq k\leq {\overline {R}}(W)\right\}}$ 。例如在图 2 中，字符串 ‘go’ 的 SA 区间为 [1, 2]。此区间中的后缀数组值为 3 和 0，给出了所有“go”出现的位置。

知道后缀数组中的间隔可以得到位置。因此，序列比对相当于搜索X的子串的SA区间与查询匹配。对于精确匹配问题，只能找到一个这样的区间；对于不精确匹配的问题，可能有很多。

精确匹配：向后搜索

令 C(a) 是 C(a)=#{0≤j≤n−2:X[j]<a}和O(a,i)=#{0≤j≤i:B[j]<a}中按字典顺序小于 a ∈ Σ 的符号数，O(a, i) 是 a 在 B[0, i] 中的出现次数。 Ferragina 和 Manzini (2000) 证明了如果 W 是 X 的子串：

${\underline {R}}(aW)=C(a)+O(a,{\underline {R}}(W)-1)+1$ (3)

${\overline {R}}(aW)=C(a)+O(a,{\overline {R}}(W))$ (4)

当且仅当 aW 是 X 的子串时， ${\underline {R}}(aW)\leq {\overline {R}}(aW)$ 。此结果使得可以通过迭代计算 ${\underline {R}}$ 和 ${\overline {R}}$ 来测试 W 是否是 X 的子串并计算 W 在 O(|W|) 时间内的出现次数从W结尾。这个过程叫做反向搜索。

需要注意的是，等式（3）和（4）实际上实现了对X的前缀trie的自顶向下遍历，因为如果知道其父节点的间隔，可以在恒定时间内计算出子节点的SA间隔 . 从这个意义上说，向后搜索相当于前缀树上的精确字符串匹配，但没有明确地将树放入内存中。

不精确匹配：有界遍历/回溯

给出了一种递归算法，用于搜索 X 的子串的 SA 区间，该区间与查询字符串 W 匹配且差异不超过 z（不匹配或间隙）。本质上，该算法使用向后搜索从基因组中采样不同的子串。此过程受 D(·) 数组的限制，其中 D(i) 是 W[0, i] 中差异数量的下限。 D 估计得越好，搜索空间越小，算法效率越高。通过为所有 i 设置 D(i)=0 来实现一个朴素的界限，但由此产生的算法在差异数量上显然是指数级的，并且效率较低。

Precalculation:
	Calculate BWT string B for reference string X
	Calculate array C(·) and Ο(·,·) from B
	Calculate BWT string B' for the reverse reference
	Calculate array Ο'(·) from B'
Procedures:
	INEXACTSEARCH(W,z)
		CalculateD(W) 
		return InexRecur(W, |W|-1,z,1,|X|-1)
	CalculateD(W)
		k ← 1
		z ← 0
		for i = 0 to |W|-1 do
			k ← C(W[i])+O'(W[i],k-1)+1
			l ← C(W[i])+O'(W[i],l)
			if k > l then
				k ← l
				l ← |X|-1 
				z ← z+1
				D(i) ← z
	InexRecur( W, z, k, l)
		if z < D(i) then
			return Φ 
		if z <0 then 
			return {[k,l]}
		I ← Φ
		I ← I ∪ InexRecur(W, i-1,z-1,k,l) 
		for each b∈{A,C,G,T} do
			k ← C(b) + O(b,k-1)+1
			l ← C(b)+O(b,l)
            if k ≤ l then
            	I ← I ∪ InexRecur(W,i,z-1,k,l) 
            	if b = W[i] then
            		I ← I ∪ InexRecur(W,i- 1 ,z,k,l) 
            	else
            		I ← I ∪ InexRecur(W,i-1 ,z-1,k,l) 
      return I

图3：不精确搜索匹配 W 的子串的 SA 区间的算法。参考 X 以 $ 终止，而 W 以 A/C/G/T 终止。过程 InexactSearch(W, z) 返回与 W 匹配的子串的 SA 间隔，差异不超过 z（不匹配或间隙）； InexRecur(W, i, z, k, l) 在后缀Wi+1匹配区间[k, l]的条件下，递归计算匹配W[0, i]且差异不超过z的子串的SA区间。以星号开头的行分别用于插入和删除 X。 D(i) 是字符串 W[0, i] 中差异数量的下限。图 3 中的 CalculateD 过程提供了一个更好但不是最佳的界限。它在概念上与图 4 中描述的相同，后者更易于理解。使用反向（未补码）参考序列的 BWT 来测试 W 的子串是否也是 X 的子串。请注意，单独使用 BWT 字符串 B 进行此测试将使CalculateD 成为 ${\textstyle O(|W|^{2})}$ O(|W|2) 过程，而不是图 3 中描述的 ${\textstyle O(|W|)}$ 。

CalculateD(W) 
	z ← 0
	j ← 0
	for i=0 to |W| — 1 do
		if W[j,i] is not a substring of X then 
			z ← z+1
			j ← i+l
			D(i) ← z

图4：计算 D(i) 的等效算法。

为了理解D的作用，回到在X=GOOGOL$中搜索W=LOL的例子（图1）。如果为所有 i 设置 D(i)=0 并禁止间隙（去除算法中的两条星线），则 InexRecur 的调用图是一棵树，有效地模仿了图 1 中虚线所示的搜索路线. 然而，通过CalculateD，知道D(0)=0 和D(1)=D(2)=1。然后可以避免下降到前缀树中的“G”和“O”子树以获得更小的搜索空间。

图 3 中的算法保证找到所有允许最大 z 差异的区间。理论上是完整的，但在实践中，也做了各种修改。首先，对不匹配、间隙开放和间隙扩展支付不同的惩罚，这对生物数据更现实。其次，使用类似堆的数据结构来保持部分命中而不是使用递归。堆状结构优先于部分命中的对齐分数，以使 BWA 始终首先找到最佳间隔。同时处理反向互补读取序列。请注意，图 3 中描述的递归有效地模拟了前缀树上的深度优先搜索 (DFS)，而 BWA 使用这种类似堆的数据结构实现了广度优先搜索 (BFS)。第三，采用迭代策略：如果顶部区间是重复的，默认不搜索次优区间；如果顶部间隔是唯一的并且具有 z 差异，则只搜索最多具有 z + 1 差异的命中。这种迭代策略在保持生成映射质量的能力的同时加速了 BWA。然而，这也使得 BWA 的速度对读取和参考之间的不匹配率敏感，因为找到具有更多差异的命中通常更慢。第四，允许对读取的前几十个碱基对的最大允许差异设置限制，称之为种子序列。给定 70 bp 模拟读数，与 32 bp 种子中最大两个差异的比对比没有种子快 2.5 倍。对齐错误率，即模拟中置信映射中错误对齐的比例（另见第 2.3.3 节），仅从 0.08% 增加到 0.11%。对于较短的读取，播种效果较差。

降低内存

上述算法需要在内存中加载出现数组O和后缀数组S。保存完整的 O 和 S 数组需要巨大的内存。幸运的是，可以通过只存储 O 和 S 数组的一小部分并动态计算其余部分来减少内存。 BWT-SW（Lam 等人，2008 年）和 Bowtie（Langmead 等人，2009 年）使用了由 Ferragina 和 Manzini（2000 年）首次引入的类似策略。

给定大小为 n 的基因组，出现数组 O(·, ·) 需要 $4n[log_{2}n]$ 位，因为每个整数需要 $[log_{2}n]$ 位，并且数组中有 4n 个。在实践中，在内存中存储 O(·, k) 的 k 为 128 的因子，并使用 BWT 字符串 B 计算其余元素。当使用两位表示核苷酸时，B 需要 2n 位。因此，用于反向搜索的内存为 2n+n⌈log2n⌉/32 $2n+n[log_{2}n]/32$ 位。由于还需要存储反向基因组的 BWT 来计算边界，因此计算间隔所需的内存增加了一倍，或者对于 3 Gb 基因组大约需要 2.3 GB。

枚举每个出现的位置需要后缀数组 S。如果将整个 S 放在内存中，它将使用 n⌈log2n⌉ 位。然而，当知道其中的一部分时，也可以重建整个 S。事实上，S 和逆压缩后缀数组 (inverse CSA) $\psi ^{-1}$ (Grossi and Vitter, 2000) 满足：

$S(k)=S((\psi ^{-1})^{(j)}(k))+j$ (5)

其中 $(\psi ^{-1})^{(j)}$ 表示将变换 $\psi ^{-1}$ 重复应用 j 次。逆 CSA $\psi ^{-1}$ 可以用出现数组 O 计算：

${\psi ^{-1}}(i)=C(B[i]+O(B[i],i)$ (6)

在 BWA 中，只在内存 S(k) 中存储可以被 32 整除的 k。对于不是 32 的因数的 k，重复应用 $\psi ^{-1}$ 直到对于某些 j， $(\psi ^{-1})^{(j)}(k)$ 是 32 的因数，然后可以查找 $S((\psi ^{-1})^{(j)}(k))$ 并且可以使用等式 (5) 计算 S(k)。

总之，比对过程使用 4n+n⌈log2n⌉/8 $4n+n[log_{2}n]/8$ 位，或 n 个字节用于小于 4 Gb 的基因组。这包括原始和反向基因组的 BWT 字符串、部分出现数组和部分后缀数组的内存。此外，堆、缓存和其他数据结构需要几百兆字节的内存。

Illumina read的其他实际问题

不明确的碱基

read上的非 A/C/G/T 碱基被简单地视为不匹配，这在算法中是隐含的（图 3）。参考基因组上的非 A/C/G/T 碱基被转换为随机核苷酸。这样做可能会导致错误命中充满模糊碱基的区域。幸运的是，鉴于相对较长的读取时间，发生这种情况的可能性非常小。尝试了 200 万个 32 bp 的读数，但没有看到任何读数偶然映射到 poly-N 区域。

双端映射

BWA 支持双端映射。它首先找到所有好的命中的位置，根据染色体坐标对它们进行排序，然后对所有潜在的命中进行线性扫描以配对两端。计算所有染色体坐标需要经常查找后缀数组。这种配对过程非常耗时，因为使用上述方法即时生成完整的后缀数组非常昂贵。为了加速配对，缓存了大的间隔。此策略将花费在配对上的时间减半。

在配对中，BWA 批量处理 256K 读取对。在每个批次中，BWA 将完整的 BWA 索引加载到内存中，为每次出现生成染色体坐标，从两端映射的映射质量高于 20 的读取对估计插入大小分布，然后将它们配对。之后，BWA 从内存中清除 BWT 索引，加载 2 位编码参考序列，并对未映射的读取执行 Smith-Waterman 对齐，其配偶可以可靠地对齐。 Smith-Waterman 对齐挽救了一些差异过大的读取。

确定允许的最大差异数

给定长度为 m 的读取，BWA 仅容忍最多具有 k 个差异（错配或间隙）的命中，其中选择 k 使得 <4% 的 m 长读取和 2% 的统一碱基错误率可能包含大于 k 的差异.使用此配置，对于 15–37 bp 读取，k 等于 2；对于 38–63 bp，k=3；对于 64–92 bp，k=4；对于 93–123 bp，k=5；对于 124–156 bp 读数，k=6。

生成映射质量分数

对于每个比对，BWA 计算一个映射质量分数，这是比对不正确的 Phred 标度概率。该算法与 MAQ 相似，不同之处在于在 BWA 中假设总能找到真正的命中。进行此修改是因为知道 MAQ 的公式高估了错过真正命中的概率，从而导致低估了映射质量。模拟表明，由于这种修改，BWA 可能会高估映射质量，但偏差相对较小。例如，BWA 在映射质量为 60 的 1 569 108 个模拟 70 bp 读数中错误地对齐了 11 个读数。这些 Q60 映射的错误率 7 × 10−6 (= 11/1 569 108) 高于理论预期 10^-6。

SOLiD read的比对

对于 SOLiD 读取，BWA 将参考基因组转换为二核苷酸“颜色”序列，并为颜色基因组构建 BWT 索引。读取被映射在颜色空间中，其中序列的反向补码与反向相同，因为颜色的补码是它本身。对于SOLiD配对末端作图，如果两种情况中的任何一种为真，则称读数对处于正确的方向：（i）两端都映射到基因组的正向链，其中R3读数具有较小的坐标； (ii) 两端映射到基因组的反向链，F3 读数具有较小的坐标。 Smith-Waterman 对齐也在色彩空间中完成。

比对后，BWA 使用动态编程将颜色读取序列解码为核苷酸序列。给定核苷酸参考子序列 $b_{1}b_{2}...b_{l+1}$ 和映射到该子序列的颜色读取序列 $c_{1}c_{2}...c_{l}$ ，BWA 推断出核苷酸序列 ${\hat {b}}_{1}{\hat {b}}_{2}...{\hat {b}}_{l+1}$ 。

$\textstyle \sum _{i=1}^{l+1}\displaystyle q^{\prime }\cdot (1-\delta _{{\hat {b}}_{i},b_{i}})+\textstyle \sum _{i=1}^{l}\displaystyle q_{i}[1-\delta _{{\hat {c}}_{i},g({\hat {b}}_{i},{\hat {b}}_{i+1})}]$

其中 q' 是突变的 Phred 标度概率，q_i 是颜色 c_i 的 Phred 质量，函数 g(b, b')=g(b', b) 给出对应于两个相邻核苷酸 b 和 b' 的颜色。本质上，如果 $b_{i}\neq {\hat {b}}_{i}$ ，将支付惩罚 q′。和一个惩罚 qi 如果 $c_{i}\neq g({\hat {b}}_{i},{\hat {b}}_{i+1})$ 。

这种优化可以通过动态编程来完成，因为超出位置 i 的最佳解码仅取决于选择 ${\hat {b}}_{i}$ 。 Let $f_{i}({\hat {b}}_{i})$ 是达到 i 的最佳解码分数。迭代方程为

$f_{1}({\hat {b}}_{1})=q^{\prime }\cdot (1-\delta _{{\hat {b}}_{i},b_{i}})$

$f_{i+1}({\hat {b}}_{i+1})=min_{{\hat {b}}_{i}}\left\{f_{i}({\hat {b}}_{i})+q^{\prime }\cdot (1-\delta _{{\hat {b}}_{i+1},b_{i+1}})+q_{i}\cdot [1-\delta _{c_{i},g({\hat {b}}_{i},{\hat {b}}_{i+1})}]\right\}$

BWA 近似基本质量如下。 Let 一个包含图片、插图等的外部文件。

对象名称是 btp324i11.jpg $c_{i}=g({\hat {b}}_{i},{\hat {b}}_{i+1})$ 。第 i 个基本质量 ${\hat {q}}_{i}$ ，i=2…l，计算如下：

$f(n)={\begin{cases}q_{i-1}+q_{i}&{\text{if }}c_{i-1}={\hat {c}}_{i-1}{\text{ and }}c_{i}={\hat {c}}_{i}\\q_{i-1}-q_{i}&{\text{if }}c_{i-1}={\hat {c}}_{i-1}{\text{ but }}c_{i}\neq {\hat {c}}_{i}\\q_{i}-q_{i-1}&{\text{if }}c_{i}={\hat {c}}_{i}{\text{ but }}c_{i-1}\neq {\hat {c}}_{i-1}\\0&{\text{otherwise}}\\\end{cases}}$

BWA 输出序列 ${\hat {b}}_{2}....{\hat {b}}_{l}$ ，质量为 ${\hat {q}}_{2}....{\hat {q}}_{l}$ 作为 SOLiD 映射的最终结果。

结果

说明

基于参考基因组的 BWT 实现了 BWA 来进行短读比对。为单端读取执行缺口比对，支持双端比对，生成比对质量并在需要时提供多次命中。默认的输出对齐格式是 SAM（序列比对/映射格式）。可以使用 SAMtools (http://samtools.sourceforge.net) 来提取区域中的比对、合并/排序比对、获得单核苷酸多态性 (SNP) 和 indel 调用并可视化比对。

文档和源代码可在 MAQ 网站免费获得：http://maq.sourceforge.net。

评估

为了评估 BWA 的性能，测试了另外三个比对程序：MAQ（Li 等人，2008a）、SOAPv2（http://soap.genomics.org.cn）和 Bowtie（Langmead 等人，2009 年）。 MAQ 索引使用哈希表read并扫描基因组，是之前为大规模read比对开发的软件包。 SOAPv2 和 Bowtie 是另外两个基于 BWT 的短读比对软件。最新的 SOAP-2.1.7（Li 等人，未公开数据）使用 2way-BWT（Lam 等人，未公开数据）进行对齐。可以接收超过 35 bp 种子序列的更多错配，并支持仅限于一个缺口开放的缺口比对。 Bowtie（版本 0.9.9.2）部署了与 BWA 类似的算法，并没有通过用 D(i) 限制搜索来减少搜索空间，而是通过巧妙地对原始和反向读取序列进行对齐以绕过对前缀树的根进行不必要的搜索。默认情况下，Bowtie 对前缀 trie 执行 DFS，并在找到第一个符合条件的命中时停止。因此，即使其播种策略被禁用，它也可能会错过最佳的不精确命中。可以通过在命令行应用“--best”来使 Bowtie 执行 BFS，但这会使 Bowtie 变慢。

包括 BWA 在内的所有四个程序都会在多个同样最佳的位置上随机放置重复读取。由于主要对实践中的置信比对感兴趣，因此需要排除重复命中。 SOAPv2 给出读取的同等最佳命中数。仅保留唯一映射。还要求 SOAPv2 将可能的间隙大小限制为最多 3 bp。使用命令行选项“--best -k 2”运行 Bowtie，使 Bowtie 输出读取的前两个命中。如果第二个最佳命中包含与最佳命中相同数量的不匹配，则丢弃读取对齐。 MAQ 和 BWA 生成映射质量。使用 MAQ 的比对质量阈值 1 和 BWA 的 10 来确定可信映射。使用不同的阈值是因为知道 MAQ 的映射质量被低估了，而 BWA 的映射质量被高估了。

模拟数据评估

使用 SAMtools 包中包含的 wgsim 程序模拟来自人类基因组的读数，并运行四个程序将读数比对回人类基因组。由于知道每个read的确切坐标，能够计算比对错误率。

表 1 显示 BWA 和 MAQ 实现了相似的比对精度。在可信映射读取的比例和可信映射的错误率方面，BWA 比 Bowtie 和 SOAPv2 更准确。请注意，SOAP-2.1.7 针对长度超过 35 bp 的读取进行了优化。对于 32 bp 读取，SOAP-2.0.1 优于最新版本。

表1：模拟数据的评估结果
	Single-end			Paired-end
Program	Time (s)	Conf (%)	Err (%)	Time (s)	Conf (%)	Err (%)
Bowtie-32	1271	79.0	0.76	1391	85.7	0.57
BWA-32	823	80.6	0.30	1224	89.6	0.32
MAQ-32	19797	81.0	0.14	21589	87.2	0.07
SOAP2-32	256	78.6	1.16	1909	86.8	0.78
Bowtie-70	1726	86.3	0.20	1580	90.7	0.43
BWA-70	1599	90.7	0.12	1619	96.2	0.11
MAQ-70	17928	91.0	0.13	19046	94.6	0.05
SOAP2-70	317	90.3	0.39	708	94.5	0.34
bowtie-125	1966	88.0	0.07	1701	91.0	0.37
BWA-125	3021	93.0	0.05	3059	97.6	0.04
MAQ-125	17506	92.7	0.08	19388	96.3	0.02
SOAP2-125	555	91.5	0.17	1187	90.8	0.14
分别从人类基因组模拟了 100 万对 32、70 和 125 bp 读数，SNP 突变率为 0.09%，indel 突变率为 0.01%，均匀测序碱基错误率为 2%。 32 bp 读数的插入大小来自正态分布 N(170, 25)，70 和 125 bp 读数来自 N(500, 50)。表中显示了 2.5 GHz Xeon E5420 处理器单核上的 CPU 时间（时间）、置信映射读取百分比 (Conf) 和置信映射错误对齐百分比 (Err)。

在速度上，SOAPv2 是最快的，如果禁用间隙对齐，双端映射实际上会快 30-80%。带有默认选项（数据未显示）的 Bowtie 比单端映射上的当前设置“–best -k 2”快几倍。但是，速度的提高是以牺牲准确性为代价的。例如，使用默认选项，Bowtie 可以在 151 秒内映射 200 万个单端 32 bp 读数，但 6.4% 的置信映射是错误的。这种高对齐错误率可能会使结构变异的检测复杂化，并可能影响 SNP 的准确性。在 BWA 和 MAQ 之间，BWA 快 6–18 倍，具体取决于读取长度。 MAQ 的速度不受读取长度的影响，因为它在内部将所有读取视为 128 bp。通过不检查类似于 Bowtie 和 SOAPv2 所做的次优命中，可以加速 BWA。然而，在这种情况下，计算映射质量是不可能的，相信生成适当的映射质量对各种下游分析有用，例如检测结构变化。

在内存上，SOAPv2 使用 5.4 GB。 Bowtie 和 BWA 都使用 2.3 GB 用于单端映射，大约 3 GB 用于双端映射，比 MAQ 的内存占用 1 GB 大。然而，所有三个基于 BWT 的对齐器的内存使用与要对齐的读取数量无关，而 MAQ 在其中是线性的。此外，所有基于 BWT 的对齐器都支持多线程，这减少了多核计算机上每个 CPU 内核的内存。在现代计算机服务器上，内存不是基于 BWT 的对齐器的实际问题。

真实数据评估

为了评估真实数据的性能，从欧洲读取档案 (AC:ERR000589) 下载了大约 1220 万对 51 bp 读取。这些读数由 Illumina 为 NA12750 生成，NA12750 是 1000 基因组计划 (http://www.1000genomes.org) 中的一个男性。读数被映射到人类基因组 NCBI build 36。表 2 显示几乎所有来自 MAQ 和 BWA 的可信比对都以一致的对存在，尽管 MAQ 给出的可信比对较少。较慢的 BWA 模式（无种子；即使最高命中是重复也搜索次优命中）效果更好。在该模式下，BWA 在 6.3 小时内自信地映射了所有读数的 89.2%，并以一致对的方式准确映射了 99.2%。

表2：真实数据评估
Program	Time (h)	Conf (%)	Paired (%)
Bowtie	5.2	84.4	96.3
BWA	4.0	88.9	98.8
MAQ	94.9	86.1	98.7
SOAP2	3.4	88.3	97.5
1220 万个读取对被对到人类基因组。 2.5 GHz 至强 E5420 处理器单核上的 CPU 时间（时间）、置信度映射读取百分比 (Conf) 和以正确方向映射且在 300 bp 范围内的配对置信度映射（配对），显示在桌子。

在这个实验中，如果间隙对齐被禁用，SOAPv2 的速度将提高两倍，置信度映射 (Conf) 和配对百分比 (Paired) 均下降 1%。相比之下，BWA 仅执行无间隙对齐时的速度是它的 1.4 倍。但即使禁用了基于 BWT 的缺口比对，BWA 仍然能够通过 Smith-Waterman 比对恢复许多短插入缺失，给出配对末端读数。

还获得了鸡基因组序列（2.1 版），并将这 1220 万个读取对与人鸡杂交参考序列进行比对。与纯人类对齐相比，置信度映射百分比几乎没有变化。至于映射到鸡基因组的读取数，Bowtie 将 2640、BWA 2942、MAQ 3005 和 SOAPv2 映射到错误的基因组的读取数为 4531。如果考虑鸡序列占人鸡杂交参考的四分之一，则 BWA 的比对错误率约为 0.06%（=2942×4/12.2M/0.889）。请注意，这种比对错误率的估计可能会被低估，因为错误比对的人类read往往与人类的重复序列相关，并比对回人类序列。由于存在高度保守的序列和人类组装不完整或鸡基因组组装错误，估计也可能被高估。

如果想要更少的错误，BWA 和 MAQ 生成的映射质量允许选择精度更高的对齐。如果将确定 BWA 的置信命中的比对质量阈值提高到 25，则 86.4% 的读数可以与比对到鸡基因组的 1927 个读数可靠地对齐，在百分比置信映射和比对到的读数数量方面均优于 Bowtie错误的基因组。

讨论

对于与人类参考基因组的短读比对，BWA 比 MAQ 快一个数量级，同时实现相似的比对精度。它支持单端读取的间隙对齐，当读取变得更长并且倾向于包含插入缺失时，这一点变得越来越重要。 BWA 以 SAM 格式输出对齐，以利用 SAMtools 中实施的下游分析。 BWA 加 SAMtools 提供了 MAQ 包的大部分功能和附加功能。

与速度、内存和比对读取的数量相比，在真实数据上评估对齐精度要困难得。本文使用了三个标准来评估比对软件的准确性。第一个标准只能用模拟数据进行评估，它是置信比对数量和置信比对中比对错误率的组合。请注意，仅可信比对的数量可能不是一个好的标准：可以以牺牲准确性为代价比对更多。第二个标准是比对read的数量和比对成一致对的read数量的组合，它适用于真实数据，假设来自实验的交配信息是正确的，并且结构变异很少。尽管此标准与比对软件定义配对“一致性”的方式有关，但根据经验，如果配对参数设置正确，则具有很高的信息量。第三个标准是如果有意添加来自不同物种的参考序列，read比对到错误参考序列的比例。

虽然理论上 BWA 适用于任意长的读取，但它的性能在长read上会下降，尤其是在测序错误率很高的情况下。此外，BWA 总是需要比对完整的read，从第一个碱基到最后一个（即相对于read的全局比对），但较长的read更有可能被参考基因组中的结构变异或错误组装中断，这将BWA 失败。对于长读段，可能更好的解决方案是将读段分成多个短片段，用上述算法分别比对片段，然后加入部分比对以获得读段的完整比对。

BWA-SW方法

BWA-SW算法概述

BWA-SW 为参考序列和查询序列构建 FM 索引。它隐含地表示前缀树中的参考序列，并表示前缀有向无环词图（前缀 DAWG；Blumer 等人，1985）中的查询序列，该图是从查询序列的前缀树转换而来的（算法图）。通过分别遍历参考前缀 trie 和查询 DAWG，可以在 trie 和 DAWG 之间应用动态编程。如果不应用启发式算法，这种动态编程将找到所有本地匹配项，但不会比 BWT-SW 快。在 BWA-SW 中，应用了两个启发式规则来大大加速这个过程。首先，查询 DAWG 上的遍历是在外循环中进行的，因此在不完成动态规划的情况下，知道参考前缀树中所有与查询节点匹配且得分为正的节点。基于对真实对齐往往具有高对齐分数的观察，可以在每个节点上修剪低分数匹配以限制仅围绕良好匹配的动态规划。动态规划的规模因此可以显着减少。在这个过程中可能会修剪真正的比对，但实际上，这可以通过使用启发式方法来控制，并且很少发生，因为给定长或高质量的查询序列。其次，BWA-SW 只报告在查询序列上基本上不重叠的比对，而不是给出所有重要的局部比对。它启发式地识别并丢弃包含在较长对齐中的种子，从而节省不成功种子扩展的计算时间。

符号和定义

后缀数组和 BWT

设 Σ={A, C, G, T} 是核苷酸字母表，$ 是一个在字典上比 Σ 中的所有符号都小的符号。给定一个核苷酸序列 X=a1…an−1 和 an−1=$，让 X[i]=ai 是第 i 个符号，X[i, j]=ai…aj 是 X 和 Xi=X 的子序列 [i, n−1] X 的后缀。 X 的后缀数组 S 是整数 0,..., n−1 的排列，使得 S(i)=j 当且仅当 Xj 是第 i 个字典序最小的后缀。 X 的 BWT 是 X 的排列，如果 S(i)=0，则 B[i]=$，否则 B[i]=X[S(i)−1]。

后缀数组间隔

给定一个序列 W，后缀数组 interval 或 SA interval ${\textstyle [{\underline {R}}(W),{\overline {R}}(W)]}$ 的 W 定义为

${\underline {R}}(W)=min\left\{k:W\ is\ the\ prefix\ of\ X_{S(k)}\right\}$

${\overline {R}}(W)=max\left\{k:W\ is\ the\ prefix\ of\ X_{S(k)}\right\}$

后缀数组间隔和序列比对

不精确匹配：有界遍历/回溯

调频指数

后缀数组 S、数组 C 和 O 足以在 X 中精确搜索模式。 FM-index (Ferragina and Manzini, 2000) 是三个数组的压缩表示，由压缩的 BWT 字符串 B、计算 O 和后缀数组 S 的一部分。然而，BWA-SW 使用简化的 FM 索引，其中不压缩 B 并在没有辅助数据结构的情况下存储部分出现数组 O。简化版本对于字母表非常小的 DNA 序列更有效。之前的论文 (Li and Durbin, 2009) 中介绍了有关构造的详细信息。

比对

对齐是一个元组 (W1, W2, A)，其中 W1 和 W2 是两个字符串，A 是一系列将 W2 转换为 W1 的复制、替换、插入和删除操作。插入和删除是间隙。差距和替代是差异。对齐的编辑距离等于 A 中差异的总数。

可以为给定评分系统的比对计算分数。如果 W1 和 W2 可以与正分数对齐，说 W1 匹配 W2，在这种情况下，也说 (W1, W2) 是匹配的。

如果 W1 是 W'1 的子串，则称匹配 (W1, W2) 包含在第一个序列的 (W'1, W'2) 中。同样，可以定义比对（更强的条件）之间以及比对和匹配之间的“包含”关系。

前缀树和前缀 DAWG

前缀 trie 和字符串“GOOGOL”的前缀 DAWG。 (A) 前缀树。符号‘∧’表示字符串的开始。节点中的两个数字给出了节点的 SA 间隔。 (B) 由具有相同 SA 间隔的折叠节点构建的前缀 DAWG。例如，在前缀树中，三个节点具有 SA 间隔 [4, 4]。他们的父母分别有区间 [1, 2]、[1, 2] 和 [1, 1]。在前缀 DAWG 中，[4, 4] 节点因此具有父节点 [1, 2] 和 [1, 1]。节点[4, 4]代表三个字符串'OG'、'OGO'和'OGOL'，前两个字符串是'OGOL'的前缀。 (A) 从 Li 和 Durbin (2009) 的图 1 修改而来。

字符串 X 的前缀 trie 是一棵树，每条边都标有一个符号，这样从叶子到根的路径上的符号串联给出了唯一的 X 前缀。从节点到根的边符号串联为总是 X 的子串，称为节点所代表的串。节点的SA区间定义为该节点所代表的字符串的SA区间。不同的节点可能有相同的区间，但是回顾SA区间的定义，知道这些节点所代表的字符串一定是同一个字符串的前缀，长度不同。

X 的前缀 DAWG 通过折叠具有相同间隔的节点从前缀 trie 转换而来。因此，在前缀 DAWG 中，节点和 SA 区间具有一一对应的关系，并且一个节点可能代表 X 的多个子串，落入序列中，其中每个子串都是下一个的前缀，如前一段所述。图 1 给出了一个例子。

将前缀树与前缀 DAWG 对齐

为查询序列 W 构建了一个前缀 DAWG 𝒢(W)，为参考 X 构建了一个前缀 trie 𝒯(X)。用于计算 W 和 X 之间的最佳分数的动态规划如下。当u是𝒢(W)的根，v是𝒯(X)的根时，设Guv=Iuv=Duv=0。在 𝒢(W) 中的节点 u，对于它的每个父节点 u′，计算

$I_{uv|u^{\prime }}=max\left\{I_{u^{\prime }v},G_{u^{\prime }v}-q\right\}-r$

$D_{uv|u^{\prime }}=max\left\{D_{uv^{\prime }},G_{uv^{\prime }}-q\right\}-r$

$G_{uv|u^{\prime }}=max\left\{G_{u^{\prime }v^{\prime }}+S(u^{\prime },u;v^{\prime },v),I_{u^{\prime }v^{\prime }},D_{u^{\prime }v^{\prime }},0\right\}-r$

其中 v′ 是 𝒯(X) 中 v 的父级，函数 S(u′, u; v′, v) 给出边上的符号 (u′, u) 和边上的符号 (v′, v) 和 q 和 r 分别是间隙开放和间隙扩展惩罚。 Guv、Iuv 和 Duv 的计算公式为：

$u^{*}=argmax_{u^{\prime }\in {\text{pre}}(u)}G_{u}v|u^{\prime }$

$(G_{uv},I_{uv},D_{uv})={\begin{cases}(G_{uv|u^{*}},I_{uv|u^{*}},D_{uv|u^{*}})&G_{uv|u^{*}}>0\\(-\infty ,-\infty ,-\infty )&{\text{otherwise}}\end{cases}}$

其中 pre(u) 是 u 的父节点集。 Guv 等于 u 表示的（可能是多个）子串与 v 表示的（一个）子串之间的最佳分数。如果 Guv>0，说节点 v 与 u 匹配。

动态规划是通过以反向后序（即所有父节点在子节点之前访问）以嵌套方式遍历𝒢(W) 和 𝒯(X) 来执行的。注意到一旦u不匹配v，u不匹配v的任何节点，只需要访问靠近𝒯(X)根节点的节点，无需遍历整个trie，相比之下大大减少了迭代次数到标准的 Smith-Waterman 算法，该算法总是通过整个参考序列。

标准 Smith-Waterman 的加速

与时间复杂度为 O(|X|·|W|) 的标准 Smith-Waterman 对齐相比，BWA-SW 具有更好的时间复杂度，因为它并不比时间复杂度为 O(|X|^0.628|W|) 的 BWT-SW 慢。（Lam 等人，2008 年）。这个结论是因为对于短序列比对，正在考虑多个可能的匹配与单个 uv 比较。然而，由于与遍历前缀 trie 和前缀 DAWG 相关的复杂步骤，与每次迭代相关的常数要大得多，这使得当使用 BWA-SW 扩展唯一对齐时 BWA-SW 效率低下。更有效的策略是使用 BWA-SW 查找部分匹配并应用 Smith-Waterman 算法进行扩展。在动态规划中，知道在任何对中考虑的部分匹配的数量，因为这可以从 SA 间隔的大小计算。当Guv足够好并且v的SA区间大小低于某个阈值（默认为3）时，保存(u,v)对，称为种子区间对，不要从𝒯中的v节点往更深处（X）。通过查找 X 和 W 的后缀数组，可以从种子间隔对中导出种子匹配，或简称为种子。这些种子随后由 Smith-Waterman 算法扩展。如果整个查询是一个高度重复的序列，它将完全按照上一节中描述的算法进行对齐，而不使用 Smith-Waterman 扩展。

因为提前停止动态编程以生成种子，全局最佳对齐可能包含多个种子，实际上这往往是长对齐的情况。通常对于 1 kb 比对，将有 10-20 个种子。下面将利用这一观察结果启发式地加快搜索速度。

BWT-SW 部署了类似的策略，在序列和前缀尝试之间执行动态编程以查找种子匹配，然后是 Smith-Waterman 扩展。与的算法的主要区别在于，无论 SA 间隔大小如何，一旦分数足够高，BWT-SW 就会启动 Smith-Waterman 对齐。有时，重复序列可能与人类基因组中的数千个位置匹配，每次扩展部分匹配可能很慢。

启发式加速

Z-最佳策略

到目前为止描述的算法是精确的，因为它能够提供与 Smith-Waterman 算法相同的结果。虽然在给定长参考序列的情况下，它比标准算法快得多，但对于比对大规模测序数据还不够快。更仔细的调查表明，即使对于唯一的 500 bp 查询序列，𝒯(X) 中的几百万个节点也可能与具有正比对分数的查询匹配。这些节点中的大多数是随机匹配或在短的低复杂度区域中匹配。参观所有这些都是浪费。

为了加速对齐，在外循环中遍历𝒢(W)，在内循环中遍历𝒯(X)，并且在𝒢(W) 中的每个节点u 处，只保留𝒯(X) 中匹配的前Z 个最佳得分节点u，而不是保留所有匹配的节点。这种启发式策略称为 Z-best。当然，当应用 Z-best 策略时，当错误匹配具有更高的分数时，可能会错过包含在真实对齐中的种子。但是，如果查询与引用几乎相同，则这种情况发生的频率较低。另外，如果真对齐很长并且包含很多种子，那么所有种子都是假的可能性很小。在模拟和真实数据（结果部分）中，发现即使 Z=1 也适用于高质量的 200 bp 读数（<5% 测序错误率）。将 Z 增加到 10 或更高会略微提高准确性，但会大大降低对齐速度。

为了减少对齐错误，除了前向对齐之外，还将反向查询序列与反向参考序列对齐，即反向反向对齐。理想情况下，正向-正向和反向-反向对齐应该产生相同的结果，但如果真正对齐中的种子具有低分后缀（或前缀），则正向-正向（或反向-反向）对齐可能会错过它，同时结合两轮对齐减少机会。此外，如果前向对齐中的最佳对齐包含许多种子匹配，则其为假的可能性也很小。在实现中，如果最佳对齐默认包含 5 个或更多种子，则不应用反向-反向对齐。

在 Smith-Waterman 扩展之前过滤种子

与 BLAST 一样，BLAT 和 SSAHA2 都报告了所有重要的比对或通常是数十个得分最高的比对，但这并不是读取映射中最需要的输出。通常对覆盖查询序列的每个区域的最佳比对或最好的少数比对更感兴趣。例如，假设一个 1000 bp 的查询序列由来自一条染色体的 900 bp 片段和来自另一条染色体的 100 bp 片段组成； 900 bp 片段中的 400 bp 是高度重复的序列。对于 BLAST，要知道这是一个嵌合读取，需要要求它报告 400 bp 重复的所有比对，这既昂贵又浪费，因为通常对包含在更长的唯一序列中的短重复序列的比对不感兴趣序列。在这个例子中，一个有用的输出是分别报告 900 bp 和 100 bp 片段的一个比对，并指出这两个片段是否有可能使最佳比对不可靠的次优比对。这样的输出简化了下游分析并节省了重建重复序列的详细比对的时间。

在 BWA-SW 中，如果查询上重叠区域的长度小于较短查询段长度的一半，就说两个对齐是不同的。的目标是找到一组不同的对齐方式，使集合中每个对齐方式的分数总和最大化。这个问题可以通过动态编程解决，但在的例子中，读取通常是完全对齐的，贪婪的近似会很好地工作。在实际实现中，根据对齐分数对局部对齐进行排序，从最好的一个扫描排序列表，如果它与所有保留的分数较大的对齐不同，则保留一个对齐；如果对齐 a2 被拒绝，因为它与 a1 没有区别，认为 a2 是 a1 的次优对齐，并使用此信息来近似映射质量。

因为只保留在查询序列上基本不重叠的比对，所以不妨丢弃对最终比对没有贡献的种子。可以在 Smith-Waterman 扩展之前使用另一种启发式方法检测此类种子，从而可以节省花费在不必要扩展上的时间。为了识别这些种子，将包含在条带中的种子链接起来（默认条带宽度为 50 bp）。如果在查询序列上，一条短链完全包含在一条长链中，并且短链中的种子数低于长链中种子数的十分之一，将丢弃短链中的所有种子，基于观察到在这种情况下，短链很少能比长链产生更好的对齐。与 Z-best 策略不同，这种启发式对对齐精度没有明显影响。在 1000 个 10 kb 模拟数据上，它将运行时间减半，而不会降低精度。

近似映射质量

Li，H。等。 (2008) 引入了映射质量的概念来估计查询序列被放置在错误位置的概率。如果对齐算法保证找到所有局部对齐，则映射质量仅由这些局部对齐决定。然而，随着 BWA-SW 部署启发式规则，产生错误对齐的机会也与启发式有关。为了估计 BWA-SW 比对的映射质量，拟合了一个经验公式：250·c1·c2·(S1−S2)/S1，其中 S1 是最佳比对的得分，S2 是次优比对的得分，如果对齐覆盖超过四个种子，则 c1 等于 1，否则为 0.5，如果通过正向-正向和反向-反向对齐找到最佳对齐，则 c2 等于 1，否则为 0.2。

结果

简介

BWA-SW 算法是作为 BWA 程序（Li 和 Durbin，2009）的一个组件实现的，该程序在 GNU 通用公共许可证 (GPL) 下分发。该实现将 BWA 索引和查询 FASTA 或 FASTQ 文件作为输入，并以 SAM 格式输出对齐（Li et al., 2009）。查询文件通常包含许多序列（读取）。依次处理每个查询序列，如果适用，使用多个线程。内存使用由 FM-index 主导，人类基因组约为 3.7 GB。每个查询所需的内存大致与序列长度成正比。在典型的测序读取中，总内存小于 4 GB；在一个具有 100 万个碱基对 (Mbp) 的查询序列上，峰值内存总共为 6.4 GB。

在实现中，尝试根据读取长度和测序错误率自动调整参数，使默认设置适用于不同特征的输入。这种行为对于不熟悉算法的用户来说很方便，并且有助于提高读取长度和错误率混合的性能。

模拟数据评价

在模拟数据上，从比对中知道正确的染色体坐标，并且评估很简单。

整体表现

表 1 显示了给定不同读取长度和错误率的 BLAT（v34）、BWA-SW（版本 0.5.3）和 SSAHA2（版本 2.4）的 CPU 时间、可靠对齐读取的分数和对齐错误率。除非必要，尝试使用每个对齐器的默认命令行选项。根据输入数据的特征微调选项可能会产生更好的性能。

表1：模拟数据评价
Program	Metrics	100 bp			200 bp			500 bp			1000 bp			10 000 bp
Program	Metrics	2%	5%	10%	2%	5%	10%	2%	5%	10%	2%	5%	10%	2%	5%	10%
BLAT	CPU sec	685	577	559	819	538	486	1078	699	512	1315	862	599	2628	1742	710
	Q20%	68.7	25.5	3.0	92.0	52.9	7.8	97.1	86.3	21.4	97.7	96.4	39.0	98.4	99.0	94.0
	errAln%	0.99	2.48	5.47	0.55	1.72	4.55	0.17	1.12	4.41	0.01	0.52	3.98	0.00	0.00	1.28
BWA-SW	CPU sec	165	125	84	222	168	118	249	172	152	234	168	150	158	134	120
	Q20%	85.1	62.2	19.8	93.8	88.7	49.7	96.1	95.5	85.1	96.9	96.5	95.0	98.4	98.5	98.1
	errAln%	0.01	0.05	0.17	0.00	0.02	0.13	0.00	0.00	0.04	0.00	0.00	0.00	0.00	0.00	0.00
SSAHA2	CPU sec	4872	7962	9345	1932	2236	5252	3311	8213	6863	1554	1583	3113	–	–	–
	Q20%	85.5	83.8	78.2	93.4	93.1	91.9	96.6	96.5	96.1	97.7	97.6	97.4	–	–	–
	errAln%	0.00	0.01	0.19	0.01	0.00	0.01	0.00	0.01	0.04	0.00	0.00	0.00	–	–	–
从人类基因组模拟了大约 10 000 000 bp 不同读长和错误率的数据。 20% 的错误是从几何分布（密度：0.7·0.3l−1）绘制的插入缺失长度的插入错误。这些模拟读数分别使用 BLAT（选项 -fastMap）、BWA-SW 和 SSAHA2（选项 -454，用于 100 和 200 bp 读数）与人类基因组对齐。然后将对齐的坐标与模拟坐标进行比较以查找对齐错误。在此表的每个单元格中，三个数字是 Intel E5420 2.5 GHz CPU 单核上的 CPU 秒数、映射质量大于或等于 20 (Q20) 的对齐百分比以及 Q20 对齐中的错误对齐百分比 . SSAHA2 和 BWA-SW 报告映射质量； BLAT 映射质量估计为最佳和次佳对齐分数之差除以最佳对齐分数的 250 倍（与 BWA-SW 的计算基本相同）。

从表 1 可以看出，BWA-SW 显然是最快的，在所有输入上都比 BLAT 和 SSAHA2 快几倍，并且其速度对读取长度或错误率不敏感。当查询较长或错误率较低时，BWA-SW 的准确率与 SSAHA2 相当。鉴于短且容易出错的读取，SSAHA2 更准确，尽管它必须花费更多时间来对齐此类读取。 SSAHA2 未在 10 kb 读取上进行测试，因为它最初不是为此任务设计的，因此性能不佳。带有 -fastMap 选项的 BLAT 比 SSAHA2 快，但精度较低。在默认选项下，BLAT 比 SSAHA2 慢几到几十倍。与 -fastMap 模式相比，精度更高，但总体上仍低于 BWA-SW（数据未显示）。

在内存上，BWA-SW 和 BLAT 都使用 ∼4 GB 内存。 SSAHA2 使用 2.4 GB 使用默认选项进行≥500 bp 的读取，使用 5.3 GB 使用 -454 选项进行更短的读取，这会增加哈希表中存储的种子序列的数量并因此增加内存。此外，BWA-SW 支持多线程，因此如果在多核计算机上运行，每个 CPU 内核可能占用更少的内存。 SSAHA2 和 BLAT 目前不支持多线程。

首先研究给定嵌合读数的每个对准器的行为。为此，制作了两个嵌合读数，它们都由一个染色体位置的 1000 bp 片段和另一个位置的 300 bp 片段组成。两次读取之间的主要区别在于，第二次读取中的 1000 bp 片段具有~750 bp 的重复序列，而第一次读取是高度独特的。当将两个嵌合读数与人类基因组进行比对时，BWA-SW 会根据需要报告四种比对，每个片段一个。最新的 SSAHA2 无法在两个读取中找到 300 bp 片段的对齐，尽管如果将 300 bp 片段作为单独读取对齐，它能够找到对齐。默认情况下，旧版本 (1.0.9) 能够在第一次读取中对齐 300 bp 片段，但对于第二次读取，需要切换到更彻底但速度更慢的配置，将所有命中报告到 750 bp重复。带有 -fastMap 的 BLAT 没有找到第二次读取的 300 bp 片段的对齐。在这两个例子中，只有 BWA-SW 有足够的能力来检测嵌合体。

此外，BWA-SW 很少产生高质量的假嵌合比对。例如，假设 10 000 1 kb 读数有 10% 的错误但在模拟中没有嵌合体，BWA-SW 预测 18 个嵌合读数。这些读取上错误对齐的片段的映射质量仅为 2.4（最大 11），这意味着 BWA-SW 意识到这些嵌合体是不可靠的。正如预期的那样，由于碱基错误较低，BWA-SW 产生的假嵌合读数较少。

真实数据评估

由于缺乏基本事实，对真实数据的评估变得复杂。然而，仍然可以通过比较两个对齐器的结果来评估相对准确性，使用真实对齐往往具有相当高的对齐分数的原则，因为大多数错误是由于未能找到种子而产生的。

假设使用两个对齐器 A 和 B 对齐读取并得到不同的结果。如果 A 和 B 都给出低映射质量，则对齐是不明确的，并且任何对齐是否错误都无关紧要。如果 A 的映射质量很高，而 A 的对齐分数比 B 差，则 A 对齐可能是错误的；即使A对齐分数比B好一点，A对齐也不可靠，A给出的高映射质量仍然值得怀疑。实际上，定义“稍微好一点”的对齐分数需要对分数差异设置任意阈值，因此这种评估方法是近似的。

表 2 汇总了 454 个读数，这些读数仅由一个比对器映射或映射到不同位置，并且被 BWA-SW 或 SSAHA2 指定的映射质量大于或等于 20。可以看到 BWA-SW 往往会错过高错误率的短对齐（其中 946 个），这与对模拟数据的评估一致。 SSAHA2 由于不同的原因错过了对齐。在 1188 次读取中，SSAHA2 产生明显错误的比对。通过分配低映射质量意识到这些对齐是错误的，但无论如何都错过了真正的对齐。


Condition	Count	BWA-SW			SSAHA2
Condition	Count	avgLen	avgDiff	avgMapQ	avgLen	avgDiff	avgMapQ
BWA-SW≥20; SSAHA2 unmapped	0	–	–	–	–	–	–
BWA-SW≥20 plausible; SSAHA2<20	1188	398.2	1.3%	178.4	198.3	13.1%	3.9
BWA-SW≥20 questionable	40	183.0	7.8%	41.2	280.3	9.4%	2.4
SSAHA2≥20; BWA-SW unmapped	946	–	–	–	75.4	6.3%	51.2
SSAHA2≥20 plausible; BWA-SW<20	47	129.0	9.3%	2.5	200.5	8.8%	34.4
SSAHA2≥20 questionable	185	400.2	1.7%	13.4	399.2	2.9%	216.4
从 SRR003161 中统一选择的总共 137 670 454 个读数分别用 BWA-SW 和 SSAHA2 映射到人类基因组。如果 BWA-SW 和 SSAHA2 对齐的最左侧坐标相差超过 355 bp（平均读取长度），则称读取不一致对齐。为每个比对计算一个分数，该分数等于匹配数减去三乘以比对区域中的差异（错配和缺口）数。如果从 BWA-SW 比对得出的分数减去从相同读取的 SSAHA2 比对得出的分数大于或等于 20（即 BWA-SW 比对足够好），则认为 BWA-SW 比对是合理的;否则，据说 BWA-SW 对齐是有问题的。合理的和有问题的 SSAHA2 比对以类似的方式定义。表中，‘BWA-SW≥20’表示映射质量高于20的BWA-SW比对。BWA-SW总共遗漏了993（=946+47）个比对，其中SSAHA2比对好，而SSAHA2比对好1188； 40 个 BWA-SW Q20 对齐和 185 个 SSAHA2 Q20 对齐可能是错误的。

对于这两个比对器，大多数错误对齐是由于忽略了与最佳报告对齐具有相似分数的对齐。例如，SSAHA2 将读取 SRR003161.1261578 与映射质量为 244 的 X 染色体对齐，而 BWA-SW 将其与具有相同对齐长度和编辑距离的 2 号染色体对齐。两个最佳评分比对的存在意味着无法唯一放置读取，并且高达 244 的映射质量是不准确的。 SSAHA2 提供这种高映射质量可能是因为它忽略了染色体 2 上的匹配。在这个特定示例中，BWA-SW 正确地给出了一个映射质量为零，尽管它可能会忽略其他示例中的替代匹配。

在模拟的 100 和 200 bp 读数上，带有 -454 选项的 SSAHA2 比 BWA-SW 提供更好的比对。在这个真实的数据集上，BWA-SW 更准确，可能是因为平均读取长度相对较长（355 bp）。为了证实这一推测，比较了来自运行 SRR002644 的 99 958 个读数的两个对齐器，平均读数长度为 206 bp。这次 BWA-SW 错过了 1092 个 SSAHA2 Q20 比对，并产生了 39 个有问题的比对； SSAHA2 漏掉了 325 个，产生了 10 个有问题的。 SSAHA2 在这个较短的数据集上更准确，尽管它比 BWA-SW 慢 9 倍，并且使用的内存多 40%。

讨论

BWA-SW 是一种有效的算法，用于将几百个或更多碱基对的查询序列与长参考基因组进行比对。对于长查询或低错误率的查询，其敏感性和特异性往往更高，并且在此类查询序列上，BWA-SW 的准确性可与迄今为止最准确的对齐器相媲美。此外，BWA-SW 能够检测可能由结构变化或参考错误组装引起的嵌合体，这可能对 BLAT 和 SSAHA2 构成挑战。

BWA-SW、BLAT 和 SSAHA2 都遵循种子和扩展范式。主要区别来自播种策略。 BLAT 和 SSAHA2 将短精确匹配识别为种子，通常长度为 11 或 12 bp。对于分别在长度为 L 和 l 的两个序列之间的 k-mer 种子，种子的预期数量为 L·l/4k，或者是 105 的数量级，用于与人类基因组的比对。用 Smith-Waterman 算法扩展这些种子是很昂贵的。为了减少不必要的种子扩展，BLAT 和 SSAHA2 默认都使用不重叠的种子，并且需要多个种子匹配，这对于随机序列应该可以很好地工作，但仍然涉及高度重复区域中的许多种子扩展。 BWA-SW 通过在独特区域使用一些长间隙种子解决了这个问题。在真实的生物数据上，它节省了许多不必要的种子扩展，并带来了更好的整体性能。然而，为了减少识别长种子的时间，BWA-SW 只保留了动态规划矩阵的一小部分，这可能会错过所有真正匹配的种子。这种启发式是对齐错误的主要来源，特别是对于短查询，当要对齐的序列之间只有很少的有效唯一种子时。幸运的是，在长对齐上，丢失所有种子的可能性很小。已经证明 BWA-SW 与 SSAHA2 一样有效。

BWA-SW 在几个方面与 BWT-SW 不同。首先，BWT-SW 保证找到所有本地匹配，而 BWA-SW 是一种启发式算法，它可能会错过真正的命中，但速度要快得多。其次，BWA-SW 对齐两个 FM 索引，而 BWT-SW 对齐一个序列和一个 FM 索引。为查询序列构建前缀 DAWG 可能有助于避免在查询中重复对齐相同的子字符串，从而提高理论时间复杂度。第三，BWA-SW在内循环中遍历参考前缀trie，而BWT-SW在内循环中遍历查询序列。如果没有启发式方法，BWA-SW 方法会损害性能，因为必须在遍历引用前缀树时用速度换取内存，而在外循环中遍历它会更有效。尽管如此，应用 Z-best 策略需要知道与查询子串匹配的得分最高的参考节点，而无需完成动态规划，因此仅在内部循环中遍历参考时才有效。第四，BWA-SW 只报告与查询序列基本不重叠的比对，而 BWT-SW 与 BLAST 一样，报告所有具有统计意义的比对。 BWA-SW 保留了对齐的关键信息，并生成更小更方便的输出。对于 BWT-SW，最终用户通常需要对结果进行后处理，以过滤掉许多他们不感兴趣的对齐方式。总而言之，鉴于大规模真实数据，BWA-SW 被调整为具有实际实用性。

BWA-SW 的高速主要来自两种策略：使用 FM 索引和抑制包含在更好匹配中的短重复匹配。虽然第一种策略不适用于基于哈希表的算法，例如 SSAHA2 和 BLAT，但第二种策略可以在此类程序中实现，并且可以通过节省大量构建重复对齐的时间来显着加速它们。虽然 BWT 的使用减少了重复中不必要的对齐，但与哈希表查找相比，每个 BWT 操作都带有一个很大的常量。如果基于哈希表的算法结合了其中的一些功能，那么它们仍有可能比 BWA-SW 更快。

参考文献

Altschul SF, et al. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 1997;25:3389–3402. [PMC free article] [PubMed] [Google Scholar]
Blumer A, et al. The smallest automaton recognizing the subwords of a text. Theor. Comput. Sci. 1985;40:31–55. [Google Scholar]
Burrows M, Wheeler DJ. Technical report 124. Palo Alto, CA: Digital Equipment Corporation; 1994. A block-sorting lossless data compression algorithm. [Google Scholar]
Campagna D, et al. PASS: a program to align short sequences. Bioinformatics. 2009;25:967–968. [PubMed] [Google Scholar]
Eaves HL, Gao Y. MOM: maximum oligonucleotide mapping. Bioinformatics. 2009;25:969–970. [PubMed] [Google Scholar]
Eid J, et al. Real-time DNA sequencing from single polymerase molecules. Science. 2009;323:133–138. [PubMed] [Google Scholar]
Ferragina P, Manzini G. Proceedings of the 41st Symposium on Foundations of Computer Science (FOCS 2000) IEEE Computer Society; 2000. Opportunistic data structures with applications; pp. 390–398. [Google Scholar]
Ferragina P, Manzini G. Proceedings of the 41st Symposium on Foundations of Computer Science (FOCS 2000) Redondo Beach, CA, USA: 2000. Opportunistic data structures with applications; pp. 390–398. [Google Scholar]
Grossi R, Vitter JS. Proceedings on 32nd Annual ACM Symposium on Theory of Computing (STOC 2000) ACM; 2000. Compressed suffix arrays and suffix trees with applications to text indexing and string matching; pp. 397–406. [Google Scholar]
Hon W.-K, et al. A space and time efficient algorithm for constructing compressed suffix arrays. Algorithmica. 2007;48:23–36. [Google Scholar]
Jiang H, Wong WH. SeqMap: mapping massive amount of oligonucleotides to the genome. Bioinformatics. 2008;24:2395–2396. [PMC free article] [PubMed] [Google Scholar]
Jung Kim Y, et al. ProbeMatch: a tool for aligning oligonucleotide sequences. Bioinformatics. 2009;25:1424–1425. [PMC free article] [PubMed] [Google Scholar]
Kent WJ. BLAT–the BLAST-like alignment tool. Genome Res. 2002;12:656–664. [PMC free article] [PubMed] [Google Scholar]
Lam TW, et al. Compressed indexing and local alignment of DNA. Bioinformatics. 2008;24:791–797. [PubMed] [Google Scholar]
Langmead B, et al. Ultrafast and memory-efficient alignment of short DNA sequences to the human genome. Genome Biol. 2009;10:R25. [PMC free article] [PubMed] [Google Scholar]
Lin H, et al. ZOOM! Zillions of oligos mapped. Bioinformatics. 2008;24:2431–2437. [PMC free article] [PubMed] [Google Scholar]
Lippert RA. Space-efficient whole genome comparisons with Burrows-Wheeler transforms. J. Comput. Biol. 2005;12:407–415. [PubMed] [Google Scholar]
Li H, et al. Mapping short DNA sequencing reads and calling variants using mapping quality scores. Genome Res. 2008a;18:1851–1858. [PMC free article] [PubMed] [Google Scholar]
Li R, et al. SOAP: short oligonucleotide alignment program. Bioinformatics. 2008b;24:713–714. [PubMed] [Google Scholar]
Li H, Durbin R. Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics. 2009;25:1754–1760. [PMC free article] [PubMed] [Google Scholar]
Li H, et al. The Sequence Alignment/Map format and SAMtools. Bioinformatics. 2009;25:2078–2079. [PMC free article] [PubMed] [Google Scholar]
Ma B, et al. PatternHunter: faster and more sensitive homology search. Bioinformatics. 2002;18:440–445. [PubMed] [Google Scholar]
Malhis N, et al. Slider–maximum use of probability information for alignment of short sequence reads and SNP detection. Bioinformatics. 2009;25:6–13. [PMC free article] [PubMed] [Google Scholar]
Meek C, et al. Proceedings of 29th International Conference on Very Large Data Bases (VLDB 2003) Berlin, Germany: 2003. OASIS: an online and accurate technique for local-alignment searches on biological sequences; pp. 910–921. [Google Scholar]
Morgulis A, et al. Database indexing for production megablast searches. Bioinformatics. 2008;24:1757–1764. [PMC free article] [PubMed] [Google Scholar]
Ning Z, et al. SSAHA: a fast search method for large DNA databases. Genome Res. 2001;11:1725–1729. [PMC free article] [PubMed] [Google Scholar]
Pearson WR, Lipman DJ. Improved tools for biological sequence comparison. Proc. Natl Acad. Sci. USA. 1988;85:2444–2448. [PMC free article] [PubMed] [Google Scholar]
Rumble SM, et al. SHRiMP: accurate mapping of short color-space reads. PLoS Comput. Biol. 2009;5:e1000386. [PMC free article] [PubMed] [Google Scholar]
Schatz M. Cloudburst: highly sensitive read mapping with mapreduce. Bioinformatics. 2009;25:1363–1369. [PMC free article] [PubMed] [Google Scholar]
Smith AD, et al. Using quality scores and longer reads improves accuracy of Solexa read mapping. BMC Bioinformatics. 2008;9:128. [PMC free article] [PubMed] [Google Scholar]
Weese D, et al. RazerS–fast read mapping with sensitivity control. Genome Res. 2009;19:1646–1654. [PMC free article] [PubMed] [Google Scholar]
Zhang Z, et al. A greedy algorithm for aligning DNA sequences. J. Comput. Biol. 2000;7:203–214. [PubMed] [Google Scholar]