 ∠A之度数为α:
∠A之度数为α:
sinα=对边长/斜边长
cosα=邻边长/斜边长
直角三角形中∠A之度数为α,定义:
- sinα=对边长/斜边长
- cosα=邻边长/斜边长
基本性质:
- sinα=cos(90°-α)
- 令∠B度数为β,β=90°-α,则sinα=a/c=cosβ=cos(90°-α)
- cosα=sin(90°-α)
- 令∠B度数为β,β=90°-α,则cosα=b/c=sinβ=sin(90°-α)
- sin2α+cos2α=1
- 三角函数的平方写在角度前,不写在角度后,以和“α2取sin”区分。

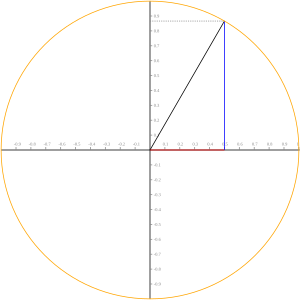 标准圆半径自x轴逆时针旋转度数为α:
标准圆半径自x轴逆时针旋转度数为α:
sinα:圆上之点的y座标
cosα:圆上之点的x座标
- sinα:标准圆上一点的 y 座标
- cosα:标准圆上一点的 x 座标
- 标准圆中的定义包含锐角直角三角形中的定义,
- 且其第一限象即为锐角直角三角形中的定义。
图形计算机:
- 画标准圆及sin、cos
- 画sin、cos图形,单位°
当α≠n×180°+90° (n×180°+90°时 cosα=0)
锐角直角三角形中的定义:
- tanα=对边长/邻边长=sinα/cosα
标准圆中的定义:
- tanα=标准圆上一点的 y 座标/x 座标=sinα/cosα
一个角度制数值所对应的弧度制数值等于单位圆中圆心角角度与该角度制数值相同时该圆心角所对应的弧长。用 表示弧度制数值,用
表示弧度制数值,用 表示角度制数值,二者转换关系为:
表示角度制数值,二者转换关系为:

常用的弧度转换公式:






- 0°
- 30°
- 45°
- 60°
- 90°
- 120°
- 180°
- 270°
- 360°
 展示余弦(或正弦)波与圆的基本关系。
展示余弦(或正弦)波与圆的基本关系。
正弦曲线常用来描写周期现象,应用非常广泛,可经常见于研究和使用于:
- 电磁波
- 信号处理的模拟信号
- 物理的简谐运动
- 声学的声音空气振动
- 乐器音叉的振动波
- 频率产生器的输出
- 交流电的电压改变
即使是其它不规则的非正弦波,其实亦能够以不同周期和波幅的“正弦波集合”来表示。这类将复杂波段化成正弦波的技术称为“傅立叶分析”。
- -α
- 90°-α
- sin(90°-α)=cosα
- cos(90°-α)=sinα
sin2α+cos2α=1
- sin(α±β)=sinαcosβ±cosαsinβ
- cos(α±β)=cosαcosβ∓sinαsinβ
图形:
- sin(A+B)图解
- sin(A-B)图解
sinα=y,cosα=x
2倍角公式
- sin2α=2xy
- cos2α=2x2-1=1-2y2=x2-y2
3倍角公式
- sin3α=3y-4y3
- cos3α=4x3-3x
5倍角公式
- sin5α=16y5-20y3+5y
- cos5α=16x5-20x3+5x
5倍角公式公式,可用来求:
- 由五倍角之正弦、余弦值等于 1 或 0 求出:
- sin36°=cos54°=

- sin54°=cos36°=

- sin18°=cos72°=

- sin72°=cos18°=

- 由 15° 的正弦、余弦值,用三倍角公式求得 5° 的正弦、余弦值,再用五倍角公式求得 1° 的正弦、余弦值。
图形计算机:
- 画二元一次联立方程式
- 多项式图形计算机,展现多段切线斜率
- 多个多项式图形计算机
方程式的解(根):
- 图形与y=0直线的交点
- x用解(根)代入,y=f(x)会得0
多项式函式的图形:
- 一次方程式:y=f(x)=mx+c,图形是直线,注意 m 正负对图形的影响
- 二次方程式:y=f(x)=ax2+bx+c,图形是抛物线,注意 a 正负对图形的影响
- 所有的抛物线形状相同
- 抛物线可描写抛物
- 抛物线可描写反射镜面
- 三次方程式:y=f(x)=4x3-3x-cos3α,(x=cosα时,y=0)
- 五次方程式:y=f(x)=16x5-20x3+5x-cos5α,(x=cosα时,y=0)
求以下诸值到小数点以下第四位(第五位四舍五入):
- √6
- √2
- sin15°
- cos15°
- sin5°
- cos5°
- sin1°
- cos1°
- sin15°、sin75°、cos15°、cos75°
- sin5°、sin85°、cos5°、cos85°
四位数三角函数表
| 角度(度) |
sin |
cos |
tan
|
| 0 |
0.0000 |
1.0000 |
0.0000
|
| 1 |
0.0175 |
0.9998 |
0.0175
|
| 2 |
0.0349 |
0.9994 |
0.0349
|
| 3 |
0.0523 |
0.9986 |
0.0524
|
| 4 |
0.0698 |
0.9976 |
0.0699
|
| 5 |
0.0872 |
0.9962 |
0.0875
|
| 6 |
0.1045 |
0.9945 |
0.1051
|
| 7 |
0.1219 |
0.9925 |
0.1228
|
| 8 |
0.1392 |
0.9903 |
0.1405
|
| 9 |
0.1564 |
0.9877 |
0.1584
|
| 10 |
0.1736 |
0.9848 |
0.1763
|
| 11 |
0.1908 |
0.9816 |
0.1944
|
| 12 |
0.2079 |
0.9781 |
0.2126
|
| 13 |
0.2250 |
0.9744 |
0.2309
|
| 14 |
0.2419 |
0.9703 |
0.2493
|
| 15 |
0.2588 |
0.9659 |
0.2679
|
| 16 |
0.2756 |
0.9613 |
0.2867
|
| 17 |
0.2924 |
0.9563 |
0.3057
|
| 18 |
0.3090 |
0.9511 |
0.3249
|
| 19 |
0.3256 |
0.9455 |
0.3443
|
| 20 |
0.3420 |
0.9397 |
0.3640
|
| 21 |
0.3584 |
0.9336 |
0.3839
|
| 22 |
0.3746 |
0.9272 |
0.4040
|
| 23 |
0.3907 |
0.9205 |
0.4245
|
| 24 |
0.4067 |
0.9135 |
0.4452
|
| 25 |
0.4226 |
0.9063 |
0.4663
|
| 26 |
0.4384 |
0.8988 |
0.4877
|
| 27 |
0.4540 |
0.8910 |
0.5095
|
| 28 |
0.4695 |
0.8829 |
0.5317
|
| 29 |
0.4848 |
0.8746 |
0.5543
|
| 30 |
0.5000 |
0.8660 |
0.5774
|
| 31 |
0.5150 |
0.8572 |
0.6009
|
| 32 |
0.5299 |
0.8480 |
0.6249
|
| 33 |
0.5446 |
0.8387 |
0.6494
|
| 34 |
0.5592 |
0.8290 |
0.6745
|
| 35 |
0.5736 |
0.8192 |
0.7002
|
| 36 |
0.5878 |
0.8090 |
0.7265
|
| 37 |
0.6018 |
0.7986 |
0.7536
|
| 38 |
0.6157 |
0.7880 |
0.7813
|
| 39 |
0.6293 |
0.7771 |
0.8098
|
| 40 |
0.6428 |
0.7660 |
0.8391
|
| 41 |
0.6561 |
0.7547 |
0.8693
|
| 42 |
0.6691 |
0.7431 |
0.9004
|
| 43 |
0.6820 |
0.7314 |
0.9325
|
| 44 |
0.6947 |
0.7193 |
0.9657
|
| 45 |
0.7071 |
0.7071 |
1.0000
|

若为任意三角形的三边,A,B,C分别为a,b,c的对角,R为此三角形的外接圆半径


证明:运用圆周角等于对同弧圆心角的一半





△=
△=
△=
 由岸边量水上船只的距离
由岸边量水上船只的距离
量水上船只距离

 ,
,



 由山脚求山高
由山脚求山高
量山高

 ,
,



请见本页图形段落










































