 ∠A之度數為α:
∠A之度數為α:
sinα=對邊長/斜邊長
cosα=鄰邊長/斜邊長
直角三角形中∠A之度數為α,定義:
- sinα=對邊長/斜邊長
- cosα=鄰邊長/斜邊長
基本性質:
- sinα=cos(90°-α)
- 令∠B度數為β,β=90°-α,則sinα=a/c=cosβ=cos(90°-α)
- cosα=sin(90°-α)
- 令∠B度數為β,β=90°-α,則cosα=b/c=sinβ=sin(90°-α)
- sin2α+cos2α=1
- 三角函數的平方寫在角度前,不寫在角度後,以和「α2取sin」區分。

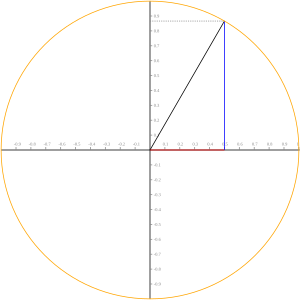 標準圓半徑自x軸逆時針旋轉度數為α:
標準圓半徑自x軸逆時針旋轉度數為α:
sinα:圓上之點的y座標
cosα:圓上之點的x座標
- sinα:標準圓上一點的 y 座標
- cosα:標準圓上一點的 x 座標
- 標準圓中的定義包含銳角直角三角形中的定義,
- 且其第一限象即為銳角直角三角形中的定義。
圖形計算機:
- 畫標準圓及sin、cos
- 畫sin、cos圖形,單位°
當α≠n×180°+90° (n×180°+90°時 cosα=0)
銳角直角三角形中的定義:
- tanα=對邊長/鄰邊長=sinα/cosα
標準圓中的定義:
- tanα=標準圓上一點的 y 座標/x 座標=sinα/cosα
一個角度制數值所對應的弧度制數值等於單位圓中圓心角角度與該角度制數值相同時該圓心角所對應的弧長。用 表示弧度制數值,用
表示弧度制數值,用 表示角度制數值,二者轉換關係為:
表示角度制數值,二者轉換關係為:

常用的弧度轉換公式:






- 0°
- 30°
- 45°
- 60°
- 90°
- 120°
- 180°
- 270°
- 360°
 展示餘弦(或正弦)波與圓的基本關係。
展示餘弦(或正弦)波與圓的基本關係。
正弦曲線常用來描寫週期現象,應用非常廣泛,可經常見於研究和使用於:
- 電磁波
- 信號處理的模擬信號
- 物理的簡諧運動
- 聲學的聲音空氣振動
- 樂器音叉的振動波
- 頻率產生器的輸出
- 交流電的電壓改變
即使是其它不規則的非正弦波,其實亦能夠以不同周期和波幅的「正弦波集合」來表示。這類將複雜波段化成正弦波的技術稱為「傅立葉分析」。
- -α
- 90°-α
- sin(90°-α)=cosα
- cos(90°-α)=sinα
sin2α+cos2α=1
- sin(α±β)=sinαcosβ±cosαsinβ
- cos(α±β)=cosαcosβ∓sinαsinβ
圖形:
- sin(A+B)圖解
- sin(A-B)圖解
sinα=y,cosα=x
2倍角公式
- sin2α=2xy
- cos2α=2x2-1=1-2y2=x2-y2
3倍角公式
- sin3α=3y-4y3
- cos3α=4x3-3x
5倍角公式
- sin5α=16y5-20y3+5y
- cos5α=16x5-20x3+5x
5倍角公式公式,可用來求:
- 由五倍角之正弦、餘弦值等於 1 或 0 求出:
- sin36°=cos54°=

- sin54°=cos36°=

- sin18°=cos72°=

- sin72°=cos18°=

- 由 15° 的正弦、餘弦值,用三倍角公式求得 5° 的正弦、餘弦值,再用五倍角公式求得 1° 的正弦、餘弦值。
圖形計算機:
- 畫二元一次聯立方程式
- 多項式圖形計算機,展現多段切線斜率
- 多個多項式圖形計算機
方程式的解(根):
- 圖形與y=0直線的交點
- x用解(根)代入,y=f(x)會得0
多項式函式的圖形:
- 一次方程式:y=f(x)=mx+c,圖形是直線,注意 m 正負對圖形的影響
- 二次方程式:y=f(x)=ax2+bx+c,圖形是拋物線,注意 a 正負對圖形的影響
- 所有的拋物線形狀相同
- 拋物線可描寫拋物
- 拋物線可描寫反射鏡面
- 三次方程式:y=f(x)=4x3-3x-cos3α,(x=cosα時,y=0)
- 五次方程式:y=f(x)=16x5-20x3+5x-cos5α,(x=cosα時,y=0)
求以下諸值到小數點以下第四位(第五位四捨五入):
- √6
- √2
- sin15°
- cos15°
- sin5°
- cos5°
- sin1°
- cos1°
- sin15°、sin75°、cos15°、cos75°
- sin5°、sin85°、cos5°、cos85°
四位數三角函數表
| 角度(度) |
sin |
cos |
tan
|
| 0 |
0.0000 |
1.0000 |
0.0000
|
| 1 |
0.0175 |
0.9998 |
0.0175
|
| 2 |
0.0349 |
0.9994 |
0.0349
|
| 3 |
0.0523 |
0.9986 |
0.0524
|
| 4 |
0.0698 |
0.9976 |
0.0699
|
| 5 |
0.0872 |
0.9962 |
0.0875
|
| 6 |
0.1045 |
0.9945 |
0.1051
|
| 7 |
0.1219 |
0.9925 |
0.1228
|
| 8 |
0.1392 |
0.9903 |
0.1405
|
| 9 |
0.1564 |
0.9877 |
0.1584
|
| 10 |
0.1736 |
0.9848 |
0.1763
|
| 11 |
0.1908 |
0.9816 |
0.1944
|
| 12 |
0.2079 |
0.9781 |
0.2126
|
| 13 |
0.2250 |
0.9744 |
0.2309
|
| 14 |
0.2419 |
0.9703 |
0.2493
|
| 15 |
0.2588 |
0.9659 |
0.2679
|
| 16 |
0.2756 |
0.9613 |
0.2867
|
| 17 |
0.2924 |
0.9563 |
0.3057
|
| 18 |
0.3090 |
0.9511 |
0.3249
|
| 19 |
0.3256 |
0.9455 |
0.3443
|
| 20 |
0.3420 |
0.9397 |
0.3640
|
| 21 |
0.3584 |
0.9336 |
0.3839
|
| 22 |
0.3746 |
0.9272 |
0.4040
|
| 23 |
0.3907 |
0.9205 |
0.4245
|
| 24 |
0.4067 |
0.9135 |
0.4452
|
| 25 |
0.4226 |
0.9063 |
0.4663
|
| 26 |
0.4384 |
0.8988 |
0.4877
|
| 27 |
0.4540 |
0.8910 |
0.5095
|
| 28 |
0.4695 |
0.8829 |
0.5317
|
| 29 |
0.4848 |
0.8746 |
0.5543
|
| 30 |
0.5000 |
0.8660 |
0.5774
|
| 31 |
0.5150 |
0.8572 |
0.6009
|
| 32 |
0.5299 |
0.8480 |
0.6249
|
| 33 |
0.5446 |
0.8387 |
0.6494
|
| 34 |
0.5592 |
0.8290 |
0.6745
|
| 35 |
0.5736 |
0.8192 |
0.7002
|
| 36 |
0.5878 |
0.8090 |
0.7265
|
| 37 |
0.6018 |
0.7986 |
0.7536
|
| 38 |
0.6157 |
0.7880 |
0.7813
|
| 39 |
0.6293 |
0.7771 |
0.8098
|
| 40 |
0.6428 |
0.7660 |
0.8391
|
| 41 |
0.6561 |
0.7547 |
0.8693
|
| 42 |
0.6691 |
0.7431 |
0.9004
|
| 43 |
0.6820 |
0.7314 |
0.9325
|
| 44 |
0.6947 |
0.7193 |
0.9657
|
| 45 |
0.7071 |
0.7071 |
1.0000
|

若為任意三角形的三邊,A,B,C分別為a,b,c的對角,R為此三角形的外接圓半徑


證明:運用圓周角等於對同弧圓心角的一半





△=
△=
△=
 由岸邊量水上船隻的距離
由岸邊量水上船隻的距離
量水上船隻距離

 ,
,



 由山腳求山高
由山腳求山高
量山高

 ,
,



請見本頁圖形段落










































