分數是指「有分子有分母的數」,本質是是乘法與除法的綜合,定義為:「除以分母,乘以分子」。就是均分為分母等份,取其分字等份。
分數的分字,含有分開、部份的意思。而拉丁文中,分數源自frangere這字,意思是打破、斷裂。
公元前1900年,巴比倫人就利用分母是60的分數來記錄數量。古埃及人也利用分數來記數,但當時記數的分數只是個符號。
其實早於商周年代,中國人已經懂得應用分數的概念,秦始皇統一中國後,擬出一年有三百六十五又四分之一天。《九章算術》是中國古代的數學理論名著,內容已提及到分數,並採用分子、分母、約分等數學名詞,我們至今仍有沿用。
在歐洲,把分數看作是兩個整數相除的商,以及分子可以大於分母數目的概念,要到16世紀才發展出來,與中國相較,遲了接近一千年。
計算分數時,商不一定是整數,在這種情況下,就要把一個單位平均分成若干分,以其中的一份或數份來表示所得的結果,這樣便產生了分數。
換句話說,分數就是把單位1平均分成若干等分後,其中1份或數份的數目。一個蛋糕平均分成3份,其中一份的數目便是 。一件薄餅平均分成5份,取去3份,就是取去
。一件薄餅平均分成5份,取去3份,就是取去 件薄餅。
件薄餅。
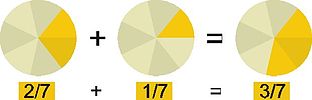
分數相加,要先通分母,分線下之數字。較易之法,為把兩個分母相乘,然後各分子亦要乘回其分母所乘之數。
例如︰

分母相乘以後,再通其分子,得以下數式


分子相加後得取結果


減法亦類似於加法,亦要先通分母。再以前者分子減去後者,得一分數,可嘗試分子分母相約以取最簡單分數。
例如︰





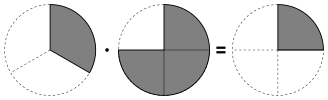
分數相乘,分子分母各自相乘,再試約簡,即為答案。



而除法,則需把後者上下顛倒,約簡後相乘即可。





可寫作帶分數。


 , (
, ( )
)





 ,(
,( )
)

- 乘是「多倍」,5×3或3×5

- 除是「均分」,15÷3為15均分為三份,每份為5
「除以分母,乘以分子」。就是均分為分母等份,取其分字等份。

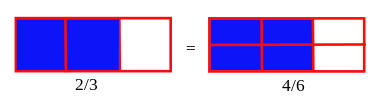
分子分母同乘以兩倍,分數大小不變。分子分母同乘以 3,4,5,6,7,8,9… 倍,分數大小還是不變。
同理,分子分母同除以兩倍,分數大小不變。分子分母同除以 3,4,5,6,7,8,9… 倍,分數大小還是不變。








整數乘以分子


整數乘以分母


分子乘以分子,分母乘以分母
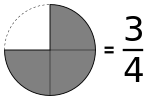
 分成四份取其三份
分成四份取其三份


 =
=

 =
=

 =
=




































































