綜合數學/實數與集合/實數和集合的基本運算

實數和集合的運算都是數學的基礎。

實數的四則運算

實數的四則運算就是實數的加、減、乘、除的總稱。

加法和減法

加法和減法是四則運算中的一級運算。
加法是基本的四則運算之一，它是指將兩個或者兩個以上的數、量合起來，變成一個數、量的計算。一般地，我們將$a$加$b$記作

$a+b$

一般讀作「$a$加$b$」或「$a$與$b$的和」。其中$a,b$我們稱作加數，「$+$」叫作加號，該式的得數我們稱作它們的和。
有$n$個數$a_{1},a_{2},\cdots ,a_{n}$的和我們一般記作

$\sum _{i=1}^{n}a_{i}$

即

$\sum _{i=1}^{n}a_{i}=a_{1}+a_{2}+\cdots a_{n}$。

減法是加法的逆運算，它指從一個數量中減去另一個數量的運算或已知兩個加數的和與其中一個加數，求另一個加數的運算。一般地，我們將$a$減$b$記作

$a-b$，

一般讀作「$a$減$b$」或「$a$與$b$的差」。其中$a$我們稱作被減數，$b$我們叫減數，「$-$」叫作減號，該式的得數我們稱作它們的差。
特殊地，$0-a$我們一般記作

$-a$，

讀作「負$a$」。這裡的「$-$」叫作負號，為了與其對應，有時也在一個數前加上「$+$」，稱作正號。$-a$和$+a$我們叫作互為相反數。 特殊地，存在

$a+0=a$，

$a-0=a$。

加法和減法在運算中優先級相同，即依據從左到右依次計算。在式子中出現括號（「$()$」，有時是「$[]$」或「$\{\}$」）時應遵循先算括號內式子的原則，當有括號相嵌時，應依據先里後外的原則進行運算。
減法與加法的關係是：減去一個數，就等於加上這個數的相反數。用字母可表示為：

$a-b=a+(-b)$，

亦有

$a+b=a-(-b)$。

證  明顯

${\begin{alignedat}{3}a-b&=a+0-b\\&=a+(0-b)\\&=a+(-b)\end{alignedat}}$，

定理得證。又有

${\begin{alignedat}{3}a+b&=a-0+b\\&=a-(0-b)\\&=a-(-b){\mbox{。 }}\end{alignedat}}$

其中$a+0-b=a+(0-b)$和$a-0+b=a+(0-b)$將在後續學習。$\blacksquare$
所以，$a-b$又可以讀作「$a$與$-b$的和」。
一般地，加法運算滿足以下運算律：

(1)加法交換律：

$a+b=b+a$；

(2)加法結合律：

$(a+b)+c=a+(b+c)$。

加法的運算律也可以推廣到減法的情形：

(1)  $a-b=-b+a$；

(2)  $(a-b)+c=a-(b-c)$，$(a+b)-c=a+(b-c)$，$(a-b)-c=a-(b+c)$。

證明略。
在加法與減法關係式的證明我們已經可以看出，在去掉括號時，一些加數的符號會發生改變。
一般地，當括號前的符號是正號時，去括號後括號內各項的符號都不發生改變；當括號前的符號是負號時，去括號後括號內各項的符號都發生改變。這就是去括號法則。用字母可以表示如下：

$\sum _{i}a_{i}+(\sum _{i}b_{i})=\sum _{i}a_{i}+\sum _{i}b_{i}$；

$\sum _{i}a_{i}-(\sum _{i}b_{i})=\sum _{i}a_{i}-\sum _{i}-b_{i}$。

證明略。

例1.2.1

計算：

(1)  $6+(4-5)$；

(2)  $9-(6+8)$；

(3)  $\sum _{i=1}^{9}(i-3)$；

(4)  $9+\left\{6-\left[7-\left(6+\sum _{i=1}^{2}-i\right)\right]\right\}$。

解  (1) 依據去括號法則，有

${\begin{alignedat}{3}{\mbox{原 式 }}&=6+4-5\\&=10-5\\&=5{\mbox{。 }}\end{alignedat}}$

或直接按順序計算

${\begin{alignedat}{3}{\mbox{原 式 }}&=6+(-1)\\&=6-1\\&=5{\mbox{； }}\end{alignedat}}$

(2)  同(1)，有

${\begin{alignedat}{2}{\mbox{原 式 }}&=9-14\\&=-5{\mbox{。 }}\end{alignedat}}$

另一解法交給讀者解答。
(3)  由定義，有

${\begin{alignedat}{3}{\mbox{原 式 }}&=(1-3)+(2-3)+(3-3)+(4-3)+(5-3)+(6-3)+(7-3)+(8-3)+(9-3)\\&=(-2)+(-1)+0+1+2+3+4+5+6\\&=18{\mbox{； }}\end{alignedat}}$

(4) 本題有較多括號，應從里至外依次計算。有

${\begin{alignedat}{5}{\mbox{原 式 }}&=9+\left\{6-\left[7-\left(6-3\right)\right]\right\}\\&=9+[6-(7-3)]\\&=9+(6-4)\\&=9+2\\&=11{\mbox{。 }}\end{alignedat}}$

乘法和除法

加法和減法是四則運算中的二級運算。
乘法是指將相同的數加起來的快捷方式。一般地，我們將$a$乘（以）$b$記為

$a\times b$，

讀作$a$乘（以）$b$或$a$與$b$的積。其中$a,b$叫作因數（或乘數），$\times$稱作乘號，它的得數叫作積。有時，為了乘號不與字母$x$相混淆，會將其記作

$a\cdot b$或$ab$。

但後者只適用於字母與字母相乘或數字與字母相乘，且數字一般置於字母之前。
若有$n$個數$a_{1},a_{2},\cdots ,a_{n}$的積我們一般記作

$\prod _{i=1}^{n}a_{i}$，

即

$\prod _{i=1}^{n}a_{i}=a_{1}a_{2}\cdots a_{n}$。

除法就是已知兩個因數的積與其中一個因數，求另一個因數的運算。一般地，我們將$a$除以$b$（或$b$除$a$）記作

$a\div b$，

讀作$a$除以$b$（或$b$除$a$）或$b$或$a$與$b$的商。其中$a$我們稱作被除數，$b$我們叫除數，「$\div$」叫作除號，該式的得數我們稱作它們的商。 但更常見地，我們會將除式寫成分數的形式或將除號寫作「$/$」，即

${\frac {a}{b}}$或$a/b$。

集合的基本運算

一般地，由集合$A$與集合$B$的所有元素構成的集合，稱為$A,B$的併集，記為

$A\cup B$，

可表示為

$A\cup B=\left\{x|x\in A\vee x\in B\right\}$。

又有，由集合$A$與集合$B$的所有公共元素構成的集合，稱為$A,B$的交集，記為

$A\cap B$，

可表示為

$A\cap B=\left\{x|x\in A\wedge x\in B\right\}$。

例1.2.2

若集合

$A=\{1,2,3\},B=\{2,3,4\}$，

求$A\cap \left(A\cup B\right)$
解 由題，有

${\begin{alignedat}{3}A\cap \left(A\cup B\right)&=\left\{1,2,3\right\}\cap \left(\left\{1,2,3\right\}\cup \left\{2,3,4\right\}\right)\\&=\left\{1,2,3\right\}\cap \left\{1,2,3,4\right\}\\&=\left\{1,2,3\right\}{\mbox{。 }}\end{alignedat}}$

對於由所有屬於集合$B$但不屬於集合$A$的元素，我們稱為集合$A$相對於$B$的相對補集，記作

$B-A$，

可表示為

$B-A=\left\{x|x\in B\wedge x\not \in A\right\}$。

特殊地，集合$A$相對於全集$U$的補集叫作絕對補集，記作

${\overline {A}}$，

可表示為

${\overline {A}}=\{x|x\not \in A\}$。

由所有屬於$A\cup B$但不屬於$A\cap B$的元素所構成的集合叫作集合$A,B$的對稱差，記作

$A\Delta B$，

可表示為

$A\Delta B=\{x|x\in A\cup B\wedge x\not \in A\cap B\}$。

關於集合運算有以下常用結論：

(1)等冪律：

$A\cap A=A,A\cup A=A$；

(2)同一律：

$A\cap I=A,A\cup I=I,A\cap \varnothing =\varnothing ,A\cup \varnothing =A$；

(3)互補律：

$A\cap {\overline {A}}=\varnothing ,A\cup {\overline {A}}=I,{\overline {\overline {A}}}=A,{\overline {I}}=\varnothing ,{\overline {\varnothing }}=I$；

(4)交換律：

$A\cap B=B\cap A,A\cup B=B\cup A$；

(5)結合律：

$A\cap (B\cap C)=(A\cap B)\cap C,A\cup (B\cup C)=(A\cup B)\cup C$；

(6)分配率：

$A\cap \left(\bigcup _{i}A_{i}\right)=\bigcup _{i}\left(A\cap A_{i}\right),A\cup \left(\bigcap _{i}A_{i}\right)=\bigcap _{i}\left(A\cap A_{i}\right)$；

(7)吸收率：

$A\cup (A\cap B)=A,A\cap (A\cup B)=A$；

(8)反演律：

${\overline {\bigcap _{i}A_{i}}}=\bigcap _{i}{\overline {A_{i}}},{\overline {\bigcup _{i}A_{i}}}=\bigcup _{i}{\overline {A_{i}}}$。

利用相關定義即可證明，略。上述運算定律在以後會有很大幫助。

容斥原理

若記有限集合$A$中的元素個數為$|A|$，則由Venn圖（下圖）可知：

1.$|A\cup B|=|A|+|B|-|A\cap B|$；

2.$|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|$。

• 
  A∪B
• 
  A∪B∪C

一般地，對於$n$個有限集合$A_{1},A_{2}\cdots ,A_{n}$，則有

$\left|\bigcup _{i=1}^{n}\right|=\sum _{k=1}^{n}\left(\left(-1\right)^{k-1}\left(\sum _{1\leqslant i_{1}<i_{2}<\cdots <i_{k}\leqslant n}\left|\bigcap _{j=1}^{k}A_{i_{j}}\right|\right)\right)$。

我們稱上述公式為容斥定理。
證 該原理可以用數學歸納法證明。
當$n=2$時，結論顯然成立。
假設命題對$n-1$成立，需證明命題對$n$也成立。
注意到$\bigcup _{i=1}^{n}A_{i}=\left(\bigcup _{i=1}^{n-1}A_{i}\right)\cup A_{n}$，由$n=2$的情形可知：

${\begin{alignedat}{2}\left|\bigcup _{i=1}^{n}A_{i}\right|&=\left|\bigcup _{i=1}^{n-1}A_{i}\right|+\left|A_{n}\right|-\left|\left(\bigcup _{i=1}^{n-1}A_{i}\right)\cap A_{n}\right|\\&=\left|\bigcup _{i=1}^{n-1}A_{i}\right|+\left|A_{n}\right|-\left|\bigcup _{i=1}^{n-1}\left(A_{i}\cap A_{n}\right)\right|{\mbox{， }}\end{alignedat}}$

由歸納假設，對於$n-1$個集合$A_{1},A_{2},\cdots ,A_{n}-1$，有

${\begin{alignedat}{2}\left|\bigcap _{i=1}^{n}\left(A_{i}\cap A_{n}\right)\right|&=\sum _{k=1}^{n-1}\left(\left(-1\right)^{k-1}\left(\sum _{1\leqslant i_{1}<i_{2}<\cdots <i_{k}\leqslant n}\left|\bigcap _{j=1}^{k}\left(A_{i_{j}}\cap A_{n}\right)\right|\right)\right)\\&=\sum _{k=1}^{n-1}\left(\left(-1\right)^{k-1}\left(\sum _{1\leqslant i_{1}<i_{2}<\cdots <i_{k}\leqslant n}\left|\left(\bigcap _{j=1}^{k}A_{i_{j}}\right)\cap A_{n}\right|\right)\right){\mbox{， }}\end{alignedat}}$

又由歸納假設，對於$n-1$個集合$A_{1},A_{2},\cdots ,A_{n}-1$，有

$\left|\bigcup _{i=1}^{n-1}A_{i}\right|=\sum _{k=1}^{n-1}\left(\left(-1\right)^{k-1}\left(\sum _{1\leqslant i_{1}<i_{2}<\cdots <i_{k}\leqslant n}\left|\bigcap _{j=1}^{k}A_{i_{j}}\right|\right)\right)$，

把上兩式代入一式，即得容斥原理。$\blacksquare$

Venn圖

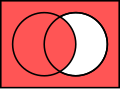
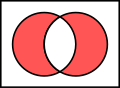
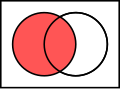
在2.3中提到的Venn圖是用於顯示元素集合重疊區域的圖示，也稱維恩圖、文氏圖。在集合論中，常常用Venn圖來表示集合間的關係或運算。
同樣的，我們之前學過的集合的關係和運算也可以用Venn圖表示如下：

• 
  U
• 
  A^C∪B^C
• 
  A∪C
• 
  A∪B^C
• 
  A Δ B
• 
  A^C∪B
• 
  B^C
• 
  A
• 
  A^C
• 
  B
• 
  A∩B^C
• 
  (A Δ B)^C
• 
  A^C∩B
• 
  A^C∩B^C
• 
  A∩B
• 
  ∅