跳至內容

三角形

維基教科書，自由的教學讀本

定義

[編輯]

不在同一直線上的三條線段首尾順次連接所組成的封閉圖形(小學-初中)；也叫三邊形。

兩平行線為一線所截(用於證明三角形內角和為180°)

[編輯]
圖一
  • 對頂角相等，如圖一，∠2=∠4、∠6=∠8
  • 同位角相等，∠α=∠β
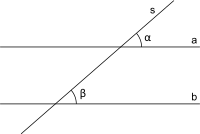
  • 內錯角相等，∠α=∠β
  • 同側內角互補，如圖一，∠4+∠5=180°，∠3+∠6=180°
    證明：
    ∵∠5+∠6=180°(平角)，∠4=∠6(內錯角)
    ∴∠4+∠5=180°。同理∠3+∠6=180°

性質

[編輯]
  1. 三角形的兩鄰邊之和大於第三邊，三角形的兩鄰邊之差小於第三邊。
    如圖，△ABC三邊為a,b,c
    ∵直線是以兩點間最短的距離，∴
    a+b>c,b+c>a,c+a>b 運用移項法則 得到
    c-a<b,c-b<a,a-b<c,
    a-c<b,b-c<a,b-a<b    		 
  2. 三角形三個內角之和等於180°。
    如圖，過C作AB的平行線，得EC
    AB、EC兩平行線，為AC所截
    ∠b=∠e(同位角相等)
    ∠a=∠d(內錯角相等)
    ∵∠c+∠e+∠d=180°(平角)∴∠a+∠b+∠c=180°
    得證△ABC三個內角加起來是180°    		 
  3. 三角形的外角等於與它不相鄰的兩個內角之和。
    設圖中的未標示內角為γ'
    ∠α+∠β+∠γ'=180°
    ∠γ+∠γ'=180°(平角)
    180°−∠γ=∠γ'
    ∠α+∠β=∠γ    		 
  4. 三角形的一個外角大於任何一個與它不相鄰的內角。
    ∵△外角等於兩遠內角之和，全體大於部分，∴外角大於任一遠內角。
  5. 三角形的三外角之和是360°。
    ∠α+∠α'=180°
    ∠β+∠β'=180°
    ∠γ+∠γ'=180°
    三式相加得：
    ∠α+∠β+∠γ+∠α'+∠β'+∠γ'=540°
    ∠α+∠β+∠γ=180°
    ∠α'+∠β'+∠γ'=540°−180°=360°    		 
  6. 同底等高的兩個三角形面積相等。
    ∵△面積=½底×高，∴同底等高的△面積皆相等。如圖
  7. 三角形的任意一條中線將這個三角形分為兩個面積相等的三角形。
    如圖，任一△的中線將原△分為紅藍兩個小△，
    ∵紅部分與藍部分之底相同(中線定義)，
    高相同(頂點到底邊只能作一條垂線)，
    ∴紅、藍兩部分兩個△面積相同。    		 

全等三角形

[編輯]

定義：經過平移、旋轉或鏡射之後，能夠完全重合的兩個三角形。

性質：

  1. 對應角相等。
  2. 對應邊相等。
  3. 面積相等。
  4. 周長相等。

重合

  1. 角相等則角之兩邊重合。
  2. 線段等長，則對應之兩端點重合，線段也重合。

三角形共有三邊與三角，兩個三角形各有六個邊、角，取三組邊或角相等共得到八種情形，可歸納為六種情形(SSA和ASS等價，AAS和SAA等價)。其中四種情形全等：

  1. SAS
  2. RHS
  3. SSS
  4. ASA
  5. AAS

一種情形ASS，又包含：

  • A為直角則兩三角形全等，稱為RHS
  • A為鈍角則兩三角形全等，沒有特別的名稱
  • A為銳角則三角形有兩種不同的形狀，不會全等

一種情形AAA代表兩三角形相似。

相關圖庫

以下討論全等條件，並簡單證明之：

SAS(邊角邊)

[編輯]

有兩邊及其夾角對應相等的兩個三角形全等。

已知△ΑΒΓ與△ΔΕΖ，∠Α=∠Δ、ΑΒ=ΔΕ、ΑΓ=ΔΖ

移動△ΔΕΖ使
Α點與Δ點重合，且∠Α與∠Δ兩邊重合(兩角相等使兩邊重合)
則Β點將與Ε點重合(線段等長兩端點重合)
同理Γ點將與Ζ點重合(線段等長兩端點重合)
∴兩△三頂點重合，兩△三邊重合，∴△ΑΒΓ≅△ΔΕΖ

等腰三角形兩底角相等

[編輯]

△ACB≅△BCA(SAS)

RHS(直角股斜邊)

[編輯]

在兩個直角三角形中，斜邊及一直角邊對應相等，那麼這兩個三角形全等。

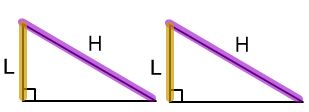
如圖依據畢氏定理：斜邊2−高2 = 另一高2
左、右兩個直角△，斜邊及一高對應相等，另一高亦會對應相等
兩個直角相等，依據SAS，左右兩個△全等。

SSS(邊邊邊)

[編輯]

三組對應邊分別相等的兩個三角形全等。

已知△ΑΒΓ與△ΔΕΖ，ΑΒ=ΔΕ、ΑΓ=ΔΖ、ΒΓ=ΕΖ

翻轉△ΑΒΓ並使ΒΓ與ΕΖ重合(兩線段相等)，且Α的位置移動到Η的位置。
△ΔΕΗ為等腰△(已知)，兩底角相等
△ΔΖΗ為等腰△(已知)，兩底角相等
∠ΕΔΖ=∠ΕΗΖ，∴△ΕΔΖ≅△ΕΗΖ(SAS)
而△ΕΗΖ是△ΑΒΓ移動並鏡射而來的，∴△ΕΔΖ≅△ΒΑΓ

ASA(角邊角)

[編輯]

有兩角及其夾邊對應相等的兩個三角形全等。

已知△ΑΒΓ與△ΔΕΖ，∠Β=∠Ε、∠Γ=∠Ζ、ΒΓ=ΕΖ

假定△ΑΒΓ與△ΔΕΖ不全等，移動△ΔΕΖ使ΒΓ與ΕΖ重合(等長)
∵∠Β=∠Ε所以Δ必落在ΑΒ線上，Α點之外的另一點Η上。
連接ΗΓ，得到∠ΗΓΒ≠∠ΑΓΒ，與已知矛盾
△ΑΒΓ必須≅△ΔΕΖ，才不致於發生矛盾

AAS(角角邊)

[編輯]
  • 有兩角及其一角的對邊對應相等的兩個三角形全等。
∵△的三角相加必等於180°，
∴若是已確定兩個角之度數，第三角之度數也必確立。
此時三角形之相等部分為AASA，已知ASA滿足全等條件，故為AAS也為全等。

ASS之討論

[編輯]

A為直角或鈍角

[編輯]

兩△全等

A為銳角

[編輯]

△只有兩種可能，並不全等。

平行四邊形

[編輯]

定義：四邊形兩組對邊平行

性質：

  1. 兩組對邊平行且相等；
  2. 兩組對角大小相等；
  3. 相鄰的兩個角互補；
  4. 對角線互相平分；
  5. 對於平面上任何一點，都存在一條能將平行四邊形平分為兩個面積相等圖形、並穿過該點的線；
  6. 四邊邊長的平方和等於兩條對角線的平方和。

中點定理和截線定理

[編輯]

中點定理：三角形兩邊中點連線平行於第三邊，且等於第三邊長的一半。

截線定理：三角形過一邊中點對底邊作平行線，平分對邊。

特殊三角形

[編輯]

定義

  1. 等邊三角形(正三角形)：三邊都相等的三角形。
  2. 等腰三角形：有兩邊相等的三角形。
  3. 直角三角形：有一個直角的三角形。
    • 特殊直角三角形：對剖正方形，對剖正三角形

性質

  1. 等邊三角形的三邊相等，且三個角都為60°。
  2. 等腰三角形的「三線」（高、中線、角平分線）合一。
  3. 等腰三角形的兩個底角都相等。
  4. 直角三角形中，兩直角邊的平方和等於斜邊的平方。
  5. 在直角三角形中，如果有一個角為30°，那麼它所對的直角邊等於斜邊的一半。
  6. 直角三角形的兩個銳角互余。
  7. 在直角三角形中，斜邊上的中線等於斜邊的一半。

判定

  1. 直角三角形。
    • 有一個角是直角的三角形是直角三角形。
    • 兩銳角互余的三角形是直角三角形。
    • 在一個三角形中，如果一邊上的中線等於這邊的一半，那麼這個三角形是直角三角形。
  2. 等腰三角形。
    • 有兩邊相等的三角形是等腰三角形。
    • 有兩個角相等的三角形是等腰三角形。
  3. 等邊三角形。
    • 三條邊都相等的三角形是等邊三角形。
    • 三個角都相等的三角形是等邊三角形。
    • 有兩邊相等，且其中一角為60°的三角形是等邊三角形。
取自 "https://zh.wikibooks.org/w/index.php?title=三角形&oldid=79777"