集合是数学中一个基本概念,本课主要学习集合。
一般地,我们把研究对象统称为元素,把一些元素组成的整体叫做集合,简称集。通常,我们用大写字母 表示集合,用小写字母
表示集合,用小写字母 表示集合中的元素。如果
表示集合中的元素。如果 是集合
是集合 的元素,我们就称
的元素,我们就称 属于集合
属于集合 ,记作
,记作 ;反之,则称
;反之,则称 不属于集合
不属于集合 ,记作
,记作 [1]。
[1]。
一般地,如果一个集合含有我们所研究问题中涉及的所有元素,那么就称这个集合为全集(通常情况下,也把给定的集合称为全集),通常记作 或
或 。
。
集合一般有两种表示法:列举法和描述法。
顾名思义,列举法就是一个一个将集合中的元素列举出来,再用“ ”将元素括起来表示集合,元素与元数之间应用“
”将元素括起来表示集合,元素与元数之间应用“ ”隔开。当元素个数过多时,可在将元素规律表示出来后用“
”隔开。当元素个数过多时,可在将元素规律表示出来后用“ ”省略后续元素。
”省略后续元素。
- 例1.6.1
用列举法表示集合 “不大于20的正奇数”,
“不大于20的正奇数”, “大于或等于10的偶数”。
“大于或等于10的偶数”。
解 这里集合 是一个有限集合,元素较少,可以完全列举;但集合
是一个有限集合,元素较少,可以完全列举;但集合 是一个无穷集合,只能用省略号省去部分元素。
是一个无穷集合,只能用省略号省去部分元素。
故

描述法是表示一个集合最常用的方法。设 为某个与
为某个与 有关的条件或法则,
有关的条件或法则, 为满足
为满足 的全体
的全体 构成的集合,则记
构成的集合,则记 为
为
 。[2]
。[2]
相应地,设 为某个与
为某个与 有关的条件或法则,
有关的条件或法则, 为满足
为满足 的全体有序数对
的全体有序数对 构成的集合,则记
构成的集合,则记 为
为
 。
。
- 例1.6.2
用描述法表示例1.1.2中的集合。
解 依题意,用描述法表示集合,则

答案不唯一。
集合有许多种,在数学上可以将集合按元素的个数分为无限集、有限集和空集,还可以按元素的类别分为数集和点集等。
顾名思义,数集就是数构成的集合,点集就是点构成的集合。我们见的最多的集合就是数集。数学中有一些特殊数集[3]:
- 由有理数和无理数构成的集合叫作实数集,记作
 ;
;
- 由整数和分数构成的集合叫作有理数集,记作
 ;
;
- 由自然数和负整数构成的集合叫作整数集,记作
 ;
;
- 由零和正整数构成的集合叫作自然数集,记作
 。有时为了明确自然数集中包括0,我们会将它记作
。有时为了明确自然数集中包括0,我们会将它记作 ;反之,不包含0的自然数集(正整数集)我们记作
;反之,不包含0的自然数集(正整数集)我们记作 ;
;
- 由除了1和它本身以外不再有其他的因数的整数构成的集合叫作质数集(有时称作素数集),记作
 ;
;
- 由形如
 的数构成的集合叫作复数集,其中
的数构成的集合叫作复数集,其中 ,
, 为虚数单位且
为虚数单位且 ,记作
,记作 ;
;
还有一些特殊数集如四元数集( )、八元数集(
)、八元数集( )和十六元数集(
)和十六元数集( )等现阶段不要求掌握,虚数集、无理数集(均用
)等现阶段不要求掌握,虚数集、无理数集(均用 表示)等有消歧义的一般不使用。
表示)等有消歧义的一般不使用。
令 是正整数的全体,且
是正整数的全体,且 ,如果存在一个正整数
,如果存在一个正整数 ,使得集合
,使得集合 与
与 一一对应,那么我们称集合A为有限集。同时定义,不含任何元素的集合称作空集,记作
一一对应,那么我们称集合A为有限集。同时定义,不含任何元素的集合称作空集,记作 。空集是特殊的有限集[4],且空集是否是点集或数集是任意的。相反地,有限集之外的集合我们叫作无限集。
。空集是特殊的有限集[4],且空集是否是点集或数集是任意的。相反地,有限集之外的集合我们叫作无限集。
集合有确定性、互异性和无序性三个性质。
给定一个集合,则哪些元素在这个集合中,哪些元素不在都应是确定的。例如“我们班个子高的学生”就不是一个集合,因为多高才叫“高个子”是不确定的,不满足集合的确定性;而“我们班身高大于170 cm的学生”是一个集合。或说,任意给定一个元素 ,则它是否属于集合
,则它是否属于集合 是确定的。
是确定的。
集合中任意两个元素都是不同的对象。如 不是一个集合,而
不是一个集合,而 才是一个集合[5]。互异性使集合中的元素是没有重复,即使两个相同的对象在同一个集合中,也只能算作这个集合的一个元素。
才是一个集合[5]。互异性使集合中的元素是没有重复,即使两个相同的对象在同一个集合中,也只能算作这个集合的一个元素。
集合中的元素排列是没有顺序的。例如,集合 。
。
以上就是集合的三个性质。
一般地,对于两个集合 ,如果集合
,如果集合 中的任何一种元素都是集合
中的任何一种元素都是集合 的元素,我们则称集合
的元素,我们则称集合 是集合
是集合 的子集,记作
的子集,记作
 (或
(或 )
)
读作“ 包含于
包含于 ”(或“
”(或“ 包含
包含 ”)。同时,如果有两个集合
”)。同时,如果有两个集合 满足
满足 且
且 ,我们则称这两个集合相等,记作
,我们则称这两个集合相等,记作
 。
。
若对于两个集合 ,有
,有
 但
但
我们则称集合 是集合
是集合 的真子集,记作[6]
的真子集,记作[6]
 (或
(或 )
)
读作“ 真包含于
真包含于 ”(或“
”(或“ 真包含
真包含 ”)。
由上述定义我们可以得到(子集的性质):
”)。
由上述定义我们可以得到(子集的性质):
- 1. 空集是任何集合的子集;
- 2. 任何集合都是它本身的子集,即
 ;
;
- 3. (集合的传递性)如果集合
 ,
,
- 则
 ;
;
- 更一般地,我们有:
- 若

- 则
 ;
;
- 4. 若集合
 中有
中有 个元素,则
个元素,则 的子集共有
的子集共有 ,真子集有
,真子集有 个。
个。
集合的相等和真子集均满足上述性质。证明略。
- 例1.6.4
列举出集合

的全部子集。
解 集合 的全部子集有:
的全部子集有:

一般地,由集合 与集合
与集合 的所有元素构成的集合,称为
的所有元素构成的集合,称为 的并集,记为
的并集,记为
 ,
,
可表示为
 。
。
又有,由集合 与集合
与集合 的所有公共元素构成的集合,称为
的所有公共元素构成的集合,称为 的交集,记为
的交集,记为
 ,
,
可表示为
 。
。
- 例1.6.5
若集合
 ,
,
求
解 由题,有

对于由所有属于集合 但不属于集合
但不属于集合 的元素,我们称为集合
的元素,我们称为集合 相对于
相对于 的相对补集,记作
的相对补集,记作
 [7],
[7],
可表示为
 。
。
特殊地,集合 相对于全集
相对于全集 的补集叫作绝对补集,记作
的补集叫作绝对补集,记作
 [8],
[8],
可表示为
 。
。
由所有属于 但不属于
但不属于 的元素所构成的集合叫作集合
的元素所构成的集合叫作集合 的对称差,记作
的对称差,记作
 ,
,
可表示为
 。
。
关于集合运算有以下常用结论:
- (1)等幂律:
 ;
;
- (2)同一律:
 ;
;
- (3)互补律:
 ;
;
- (4)交换律:
 ;
;
- (5)结合律:
 ;
;
- (6)分配率:
 ;
;
- (7)吸收率:
 ;
;
- (8)反演律:
 。
。
利用相关定义即可证明,略。上述运算定律在以后会有很大帮助。
若记有限集合 中的元素个数为
中的元素个数为 [9],则由Venn图(下图)可知:
[9],则由Venn图(下图)可知:
- 1.
 ;
;
- 2.
 。
。
一般地,对于 个有限集合
个有限集合 ,则有
,则有
 。
。
我们称上述公式为容斥定理。
证 该原理可以用数学归纳法证明。
当 时,结论显然成立。
时,结论显然成立。
假设命题对 成立,需证明命题对
成立,需证明命题对 也成立。
也成立。
注意到 ,由
,由 的情形可知:
的情形可知:

由归纳假设,对于 个集合
个集合 ,有
,有

又由归纳假设,对于 个集合
个集合 ,有
,有
 ,
,
把上两式代入一式,即得容斥原理。
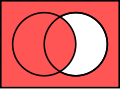
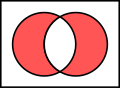
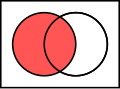
在2.3中提到的Venn图是用于显示元素集合重叠区域的图示,也称维恩图、文氏图。在集合论中,常常用Venn图来表示集合间的关系或运算。
同样的,我们之前学过的集合的关系和运算也可以用Venn图表示如下:
-
U
-
AC∪BC
-
A∪C
-
A∪BC
-
A Δ B
-
AC∪B
-
BC
-
A
-
AC
-
B
-
A∩BC
-
(A Δ B)C
-
AC∩B
-
AC∩BC
-
A∩B
-
∅
集合论中常用的实数集合为区间与邻域。
设 且
且 ,我们定义:
,我们定义:
- (1)闭区间:
![{\displaystyle [\,a,b\,]=\{x|a\leqslant x\leqslant b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a72fa4ff21f1545eaa4f1e8788b3baf2da043c8b) ;
;
- (2)开区间:
 ;
;
- (3)半开区间:
- (3.1)左开区间:
![{\displaystyle (a,b\,]=\{x|a<x\leqslant b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a13e78b93446dbcac8f75a85ff6fdf0b525518e2) ;
;
- (3.2)右开区间:
 ;
;
- (4)无穷区间:
- (4.1)
![{\displaystyle (-\infty ,b\,]=\{x|x\leqslant b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0947e255ae35cd229399b55ec7aff82334a87ac0) ;
;
- (4.2)
 ;
;
- (4.3)
 ;
;
- (4.4)
 ;
;
- (4.5)
 。
。
通常,我们将上述四类区间统称为区间。其中(1)-(3)我们称为有限区间, 分别称为区间的左端点、右端点。
分别称为区间的左端点、右端点。
设 为某个正数,则称开区间
为某个正数,则称开区间 为点
为点 的
的 邻域;称
邻域;称 为邻域的中心,
为邻域的中心, 为邻域的半径。
为邻域的半径。
点 的邻域去掉中心
的邻域去掉中心 后的集合
后的集合

称为点 的空心邻域或去心邻域;称开区间
的空心邻域或去心邻域;称开区间 为点
为点 的左邻域,
的左邻域, 为点
为点 的右邻域。
的右邻域。
点 的邻域可表示为不等式
的邻域可表示为不等式
 ;
;
点 的空心邻域可表示为不等式
的空心邻域可表示为不等式
 。
。
- ↑ 有时也将
 记作
记作 。
。
- ↑ 当描述法式子中未指明数的性质时,默认为实数。
- ↑ 有时可以用粗体字母表示特殊数集的符号。
- ↑ 由于空集不符合有限集定义,故有时不将它看作有限集。
- ↑ 有时也将含有几个相同的元素的集合视为集合,并将几个相同元素视为一个元素。
- ↑ 有时也将“
 ”写作“
”写作“ ”,多见于我国(指中华人民共和国)中学教材。
”,多见于我国(指中华人民共和国)中学教材。
- ↑ 或
 。
。
- ↑ 或
 、
、 。
。
- ↑ 有时也记为
 。
。




























































































































![{\displaystyle [\,a,b\,]=\{x|a\leqslant x\leqslant b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a72fa4ff21f1545eaa4f1e8788b3baf2da043c8b)

![{\displaystyle (a,b\,]=\{x|a<x\leqslant b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a13e78b93446dbcac8f75a85ff6fdf0b525518e2)

![{\displaystyle (-\infty ,b\,]=\{x|x\leqslant b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0947e255ae35cd229399b55ec7aff82334a87ac0)




















