綜合數學/實數及其運算/集合的基本運算

集合是數學中一個基本概念，本課主要學習集合。

集合與元素

一般地，我們把研究對象統稱為元素，把一些元素組成的整體叫做集合，簡稱集。通常，我們用大寫字母$A,B,C\cdots$表示集合，用小寫字母$a,b,c\cdots$表示集合中的元素。如果$a$ 是集合$A$ 的元素，我們就稱$a$ 屬於集合$A$，記作$a\in A$；反之，則稱$a$ 不屬於集合$A$，記作$a\not \in A$。

一般地，如果一個集合含有我們所研究問題中涉及的所有元素，那麼就稱這個集合為全集（通常情況下，也把給定的集合稱為全集），通常記作$U$或$I$。

集合的表示

集合一般有兩種表示法：列舉法和描述法。

列舉法

顧名思義，列舉法就是一個一個將集合中的元素列舉出來，再用「$\{\}$」將元素括起來表示集合，元素與元數之間應用「$,$」隔開。當元素個數過多時，可在將元素規律表示出來後用「$\cdots$」省略後續元素。

例1.6.1

用列舉法表示集合$A=$「不大於20的正奇數」，$B=$「大於或等於10的偶數」。
解 這裡集合$A$是一個有限集合，元素較少，可以完全列舉；但集合$B$是一個無窮集合，只能用省略號省去部分元素。
故

${\begin{alignedat}{2}&A=\{1,3,5,7,9,11,13,15,17,19\},\\&B=\{10,12,14,16,\cdots \}{\mbox{。 }}\end{alignedat}}$

描述法

描述法是表示一個集合最常用的方法。設$P(x)$為某個與$x$有關的條件或法則，$X$為滿足$P(x)$的全體$x$構成的集合，則記$X$為

$X=\{x|P(x)\}$。

相應地，設$P(x,y)$為某個與$x,y$有關的條件或法則，$A$為滿足$P(x,y)$的全體有序數對$(x,y)$構成的集合，則記$A$為

$A=\{(x,y)|P(x,y)\}$。

例1.6.2

用描述法表示例1.1.2中的集合。
解 依題意，用描述法表示集合，則

${\begin{alignedat}{2}&A=\{x|x=2n+1,0\leq n\leq 9,n\in \mathbb {Z} \},\\&B=\{x|x=2n,n\geq 5,n\in \mathbb {Z} \}{\mbox{。 }}\end{alignedat}}$

答案不唯一。

集合的分類

集合有許多種，在數學上可以將集合按元素的個數分為無限集、有限集和空集，還可以按元素的類別分為數集和點集等。

數集和點集

顧名思義，數集就是數構成的集合，點集就是點構成的集合。我們見的最多的集合就是數集。數學中有一些特殊數集：

由有理數和無理數構成的集合叫作實數集，記作$\mathbb {R}$；

由整數和分數構成的集合叫作有理數集，記作$\mathbb {Q}$；

由自然數和負整數構成的集合叫作整數集，記作$\mathbb {Z}$；

由零和正整數構成的集合叫作自然數集，記作$\mathbb {N}$。有時為了明確自然數集中包括0，我們會將它記作$\mathbb {N} _{0}$；反之，不包含0的自然數集（正整數集）我們記作$\mathbb {N} ^{*}$；

由除了1和它本身以外不再有其他的因數的整數構成的集合叫作質數集（有時稱作素數集），記作$\mathbb {P}$；

由形如$a+b\mathrm {i}$的數構成的集合叫作複數集，其中$a,b\in \mathbb {R}$，$\mathrm {i}$為虛數單位且$\mathrm {i} ^{2}=-1$，記作$\mathbb {C}$；

還有一些特殊數集如四元數集（$\mathbb {H}$）、八元數集（$\mathbb {O}$）和十六元數集（$\mathbb {S}$）等現階段不要求掌握，虛數集、無理數集（均用$\mathbb {I}$表示）等有消歧義的一般不使用。

無限集、有限集和空集

令$\mathbb {N} ^{*}$是正整數的全體，且$N_{n}=\{1,2,3,\cdots ,n\}$,如果存在一個正整數$n$，使得集合$A$與$N_{n}$一一對應，那麼我們稱集合A為有限集。同時定義，不含任何元素的集合稱作空集，記作$\varnothing$。空集是特殊的有限集，且空集是否是點集或數集是任意的。相反地，有限集之外的集合我們叫作無限集。

例1.6.3

判斷下列集合是什麼集合

(1)$A=\left\{x|0\leqslant x\leq 10\right\}$；

(2)$B=\left\{x|x\in \mathbb {Z} ,x^{2}\leqslant 0\right\}$；

(3)$C=\left\{x|x\in \mathbb {N} ,x<-3\right\}$；

(4)$D=\left\{\left(x,y\right)|x\geqslant y\right\}$；

解 (1)依題意，集合$A=$「大於等於0、小於等於10的（實）數」，明顯，集合$A$是無限數集；
(2)由於實數範圍內滿足$x^{2}\leq 0$的數只有0，且$0\in \mathbb {Z}$，故集合$B=\left\{0\right\}$為有限數集；
(3)明顯，自然數集內沒有小於-3的數，則$C=\varnothing$，為空集；
(4)由於集合滿足$x\geqslant y$的點有無數個，故集合$D$為一無限點集。

集合的性質

集合有確定性、互異性和無序性三個性質。

確定性

給定一個集合，則哪些元素在這個集合中，哪些元素不在都應是確定的。例如「我們班個子高的學生」就不是一個集合，因為多高才叫「高個子」是不確定的，不滿足集合的確定性；而「我們班身高大於170 cm的學生」是一個集合。或說，任意給定一個元素$a$，則它是否屬於集合$A$是確定的。

互異性

集合中任意兩個元素都是不同的對象。如$\{1,1,2\}$不是一個集合，而$\{1,2\}$才是一個集合。互異性使集合中的元素是沒有重複，即使兩個相同的對象在同一個集合中，也只能算作這個集合的一個元素。

無序性

集合中的元素排列是沒有順序的。例如，集合$\{1,3,2\}=\{1,2,3\}$。

以上就是集合的三個性質。

集合間的基本關係和運算

集合間的基本關係 

一般地，對於兩個集合$A,B$，如果集合$A$中的任何一種元素都是集合$B$的元素，我們則稱集合$A$是集合$B$的子集，記作

$A\subseteq B$（或$B\supseteq A$）

讀作「$A$包含於$B$」（或「$B$包含$A$」）。同時，如果有兩個集合$A,B$滿足$A\subseteq B$且$B\subseteq A$，我們則稱這兩個集合相等，記作

$A=B$。

若對於兩個集合$A,B$，有

$A\subseteq B$但$A\neq B$

我們則稱集合$A$是集合$B$的真子集，記作

$A\subset B$（或$B\supset A$）

讀作「$A$真包含於$B$」（或「$B$真包含$A$」）。 由上述定義我們可以得到（子集的性質）：

1. 空集是任何集合的子集；

2. 任何集合都是它本身的子集，即

$A\subseteq A$；

3. （集合的傳遞性）如果集合

$A\subseteq B,B\subseteq C$，

則

$A\subseteq C$；

更一般地，我們有：

若

$A_{1}\subseteq A_{2},A_{2}\subseteq A_{3},\cdots ,A_{n-1}\subseteq A_{n},$

則

$A_{1}\subseteq A_{n}$；

4.  若集合$A$中有$n$個元素，則$A$的子集共有$2^{n}$，真子集有$2^{n-1}$個。

集合的相等和真子集均滿足上述性質。證明略。

例1.6.4

列舉出集合

$A=\{1,2,3\}$

的全部子集。
解 集合$A$的全部子集有：

$\varnothing ,\{1\},\{2\},\{3\},\{1,2\},\{2,3\},\{1,2,3\}$

集合的相關運算

一般地，由集合$A$與集合$B$的所有元素構成的集合，稱為$A,B$的併集，記為

$A\cup B$，

可表示為

$A\cup B=\left\{x|x\in A\vee x\in B\right\}$。

又有，由集合$A$與集合$B$的所有公共元素構成的集合，稱為$A,B$的交集，記為

$A\cap B$，

可表示為

$A\cap B=\left\{x|x\in A\wedge x\in B\right\}$。

例1.6.5

若集合

$A=\{1,2,3\},B=\{2,3,4\}$，

求$A\cap \left(A\cup B\right)$
解 由題，有

${\begin{alignedat}{3}A\cap \left(A\cup B\right)&=\left\{1,2,3\right\}\cap \left(\left\{1,2,3\right\}\cup \left\{2,3,4\right\}\right)\\&=\left\{1,2,3\right\}\cap \left\{1,2,3,4\right\}\\&=\left\{1,2,3\right\}{\mbox{。 }}\end{alignedat}}$

對於由所有屬於集合$B$但不屬於集合$A$的元素，我們稱為集合$A$相對於$B$的相對補集，記作

$B-A$，

可表示為

$B-A=\left\{x|x\in B\wedge x\not \in A\right\}$。

特殊地，集合$A$相對於全集$U$的補集叫作絕對補集，記作

${\overline {A}}$，

可表示為

${\overline {A}}=\{x|x\not \in A\}$。

由所有屬於$A\cup B$但不屬於$A\cap B$的元素所構成的集合叫作集合$A,B$的對稱差，記作

$A\Delta B$，

可表示為

$A\Delta B=\{x|x\in A\cup B\wedge x\not \in A\cap B\}$。

關於集合運算有以下常用結論：

(1)等冪律：

$A\cap A=A,A\cup A=A$；

(2)同一律：

$A\cap I=A,A\cup I=I,A\cap \varnothing =\varnothing ,A\cup \varnothing =A$；

(3)互補律：

$A\cap {\overline {A}}=\varnothing ,A\cup {\overline {A}}=I,{\overline {\overline {A}}}=A,{\overline {I}}=\varnothing ,{\overline {\varnothing }}=I$；

(4)交換律：

$A\cap B=B\cap A,A\cup B=B\cup A$；

(5)結合律：

$A\cap (B\cap C)=(A\cap B)\cap C,A\cup (B\cup C)=(A\cup B)\cup C$；

(6)分配率：

$A\cap \left(\bigcup _{i}A_{i}\right)=\bigcup _{i}\left(A\cap A_{i}\right),A\cup \left(\bigcap _{i}A_{i}\right)=\bigcap _{i}\left(A\cap A_{i}\right)$；

(7)吸收率：

$A\cup (A\cap B)=A,A\cap (A\cup B)=A$；

(8)反演律：

${\overline {\bigcap _{i}A_{i}}}=\bigcap _{i}{\overline {A_{i}}},{\overline {\bigcup _{i}A_{i}}}=\bigcup _{i}{\overline {A_{i}}}$。

利用相關定義即可證明，略。上述運算定律在以後會有很大幫助。

容斥原理

若記有限集合$A$中的元素個數為$|A|$，則由Venn圖（下圖）可知：

1.$|A\cup B|=|A|+|B|-|A\cap B|$；

2.$|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|$。

• 
  A∪B
• 
  A∪B∪C

一般地，對於$n$個有限集合$A_{1},A_{2}\cdots ,A_{n}$，則有

$\left|\bigcup _{i=1}^{n}\right|=\sum _{k=1}^{n}\left(\left(-1\right)^{k-1}\left(\sum _{1\leqslant i_{1}<i_{2}<\cdots <i_{k}\leqslant n}\left|\bigcap _{j=1}^{k}A_{i_{j}}\right|\right)\right)$。

我們稱上述公式為容斥定理。
證 該原理可以用數學歸納法證明。
當$n=2$時，結論顯然成立。
假設命題對$n-1$成立，需證明命題對$n$也成立。
注意到$\bigcup _{i=1}^{n}A_{i}=\left(\bigcup _{i=1}^{n-1}A_{i}\right)\cup A_{n}$，由$n=2$的情形可知：

${\begin{alignedat}{2}\left|\bigcup _{i=1}^{n}A_{i}\right|&=\left|\bigcup _{i=1}^{n-1}A_{i}\right|+\left|A_{n}\right|-\left|\left(\bigcup _{i=1}^{n-1}A_{i}\right)\cap A_{n}\right|\\&=\left|\bigcup _{i=1}^{n-1}A_{i}\right|+\left|A_{n}\right|-\left|\bigcup _{i=1}^{n-1}\left(A_{i}\cap A_{n}\right)\right|{\mbox{， }}\end{alignedat}}$

由歸納假設，對於$n-1$個集合$A_{1},A_{2},\cdots ,A_{n}-1$，有

${\begin{alignedat}{2}\left|\bigcap _{i=1}^{n}\left(A_{i}\cap A_{n}\right)\right|&=\sum _{k=1}^{n-1}\left(\left(-1\right)^{k-1}\left(\sum _{1\leqslant i_{1}<i_{2}<\cdots <i_{k}\leqslant n}\left|\bigcap _{j=1}^{k}\left(A_{i_{j}}\cap A_{n}\right)\right|\right)\right)\\&=\sum _{k=1}^{n-1}\left(\left(-1\right)^{k-1}\left(\sum _{1\leqslant i_{1}<i_{2}<\cdots <i_{k}\leqslant n}\left|\left(\bigcap _{j=1}^{k}A_{i_{j}}\right)\cap A_{n}\right|\right)\right){\mbox{， }}\end{alignedat}}$

又由歸納假設，對於$n-1$個集合$A_{1},A_{2},\cdots ,A_{n}-1$，有

$\left|\bigcup _{i=1}^{n-1}A_{i}\right|=\sum _{k=1}^{n-1}\left(\left(-1\right)^{k-1}\left(\sum _{1\leqslant i_{1}<i_{2}<\cdots <i_{k}\leqslant n}\left|\bigcap _{j=1}^{k}A_{i_{j}}\right|\right)\right)$，

把上兩式代入一式，即得容斥原理。$\blacksquare$

Venn圖

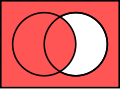
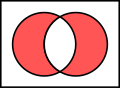
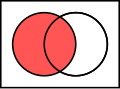
在2.3中提到的Venn圖是用於顯示元素集合重疊區域的圖示，也稱維恩圖、文氏圖。在集合論中，常常用Venn圖來表示集合間的關係或運算。
同樣的，我們之前學過的集合的關係和運算也可以用Venn圖表示如下：

• 
  U
• 
  A^C∪B^C
• 
  A∪C
• 
  A∪B^C
• 
  A Δ B
• 
  A^C∪B
• 
  B^C
• 
  A
• 
  A^C
• 
  B
• 
  A∩B^C
• 
  (A Δ B)^C
• 
  A^C∩B
• 
  A^C∩B^C
• 
  A∩B
• 
  ∅

區間與鄰域

集合論中常用的實數集合為區間與鄰域。
設$a,b\in \mathbb {R}$且$a<b$，我們定義：

(1)閉區間：$[\,a,b\,]=\{x|a\leqslant x\leqslant b\}$；

(2)開區間：$(a,b)=\{x|a<x<b\}$；

(3)半開區間：

(3.1)左開區間：$(a,b\,]=\{x|a<x\leqslant b\}$；

(3.2)右開區間：$[\,a,b)=\{x|a\leqslant x<b\}$；

(4)無窮區間：

(4.1) $(-\infty ,b\,]=\{x|x\leqslant b\}$；

(4.2) $(-\infty ,b)=\{x|x<b\}$；

(4.3) $[\,a,+\infty )=\{x|x\geqslant a\}$；

(4.4) $(a,+\infty )=\{x|x>a\}$；

(4.5)  $(+\infty ,-\infty )=\mathbb {R}$。

通常，我們將上述四類區間統稱為區間。其中(1)-(3)我們稱為有限區間，$a,b$分別稱為區間的左端點、右端點。
設$\varepsilon$為某個正數，則稱開區間$(x_{0}-\varepsilon ,x_{0}+\varepsilon )$為點$x_{0}$的$\varepsilon$鄰域；稱$x_{0}$為鄰域的中心，$\varepsilon$為鄰域的半徑。
點$x_{0}$的鄰域去掉中心$x_{0}$後的集合

$(x_{0}-\varepsilon ,x_{0})\cup (x_{0},x_{0}+\varepsilon )$

稱為點$x_{0}$的空心鄰域或去心鄰域；稱開區間$(x_{0}-\varepsilon ,x_{0})$為點$x_{0}$的左鄰域，$(x_{0},x_{0}+\varepsilon )$為點$x_{0}$的右鄰域。
點$x_{0}$的鄰域可表示為不等式

$|x-x_{0}|<\varepsilon$；

點$x_{0}$的空心鄰域可表示為不等式

$0<|x-x_{0}|<\varepsilon$。