三角形的五心

定义

三角形五心的定义

三角形的内心、外心、重心及垂心称为三角形的四心，定义如下：

名称	定义	图示	备注
内心	三个内角的角平分线的交点		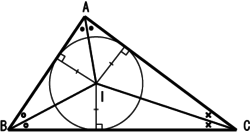该点为三角形内切圆的圆心。
外心	三条边的垂直平分线的交点		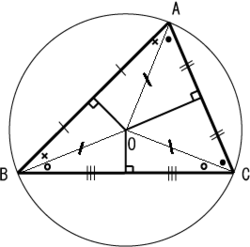该点为三角形外接圆的圆心。
重心	三条中线的交点		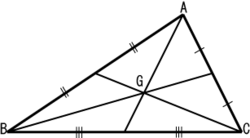被交点划分的线段比例为1:2(靠近角的一段较长)。
垂心	三条高线的交点

垂心(蓝)、重心(黄)和外心(绿)能连成一线，且成比例2:1，称为尤拉线。

连同以下的旁心，合称为三角形的五心：

名称	定义	图示	备注
旁心	其中一内角和另外两外角的角平分线的交点		有三个，为三角形某一边上的旁切圆的圆心。

正弦(sine)、余弦(Cosine)定义

∠A之度数为α：
sinα=对边长/斜边长
cosα=邻边长/斜边长

直角三角形中∠A之度数为α，定义：

sinα=对边长/斜边长

cosα=邻边长/斜边长

基本性质：

1. sinα=cos(90°-α)

   令∠B度数为β，β=90°-α，则sinα=a/c=cosβ=cos(90°-α)

2. cosα=sin(90°-α)

   令∠B度数为β，β=90°-α，则cosα=b/c=sinβ=sin(90°-α)

3. sin²α+cos²α=1

三角函数的平方写在角度前，不写在角度后，以和“α²取sin”区分。

${\sin }^2\alpha +{\cos }^2\alpha =\frac{a^2}{c^2}+\frac{b^2}{c^2}=\frac{c^2}{c^2}=1$

两大公式

(一)圆周角等于对同弧圆心角的一半

正弦定理

若$R$为外接圆半径，则 $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$。

(二)余弦定理

$c^2=a^2+b^2-2ab\cos \gamma$

$b^2=c^2+a^2-2ca\cos \beta$

$a^2=b^2+c^2-2bc\cos \alpha$

三角形面积公式

(一)已知两边及其夹角

三角形面积为二分之一两边乘以夹角正弦。

△=$\frac{1}{2}\times ab\times \sin \gamma$

△=$\frac{1}{2}\times b\times h=\frac{1}{2}\times b\times h\times \frac{a}{a}=\frac{1}{2}\times a\times b\times \frac{h}{a}=\frac{1}{2}\times ab\times \sin \gamma$

(二)海伦-秦九韶公式

$s=\frac{a+b+c}{2}$

△=$\sqrt{s(s-a)(s-b)(s-c)}$

(三)内切圆半径

$s=\frac{a+b+c}{2}$，r为内切圆半径

△面积 $=sr$

(四)外接圆半径

R为外接圆半径

△=$\frac{abc}{4R}$

证明

(六)三高

△= ½×a×h_a= ½×b×h_b= ½×c×h_c

(七)以三点坐标求面积

△=$\pm \frac{1}{2}\left|\begin{array}{cc}{x}_2-x_1& y_2-y_1\\ x_3-x_1& y_3-y_1\end{array}\right|$

如 (x₁,y₁) 为 (0,0) 即原点，则

△=$\pm \frac{1}{2}\left|\begin{array}{cc}{x}_2& y_2\\ x_3& y_3\end{array}\right|$

再旋转使 (x₃,y₃) 位于 X 轴，为 (x₃,0)。此时 x₃ 为底， y₂ 为高：

△=$\frac{1}{2}\left|\begin{array}{cc}{x}_2& y_2\\ x_3& 0\end{array}\right|=-\frac{1}{2}{x}_3{y}_2$

从一角出发，其两边的向量为 $𝐚$ 及 $𝐛$

△=$\frac{1}{2}|𝐚\times 𝐛|$