OpenSCAD用戶手冊/3D 基礎模型

立方體

在第一卦限中創建一個立方體。當center參數為true, 立方體中心點位於原點。如果按下列順序輸入參數，則參數名可寫可不寫。

cube(size = [x,y,z], center = true/false);
cube(size =  x ,     center = true/false);

參數:

size

單個值, 立方體所有邊以此為邊長

3值數組[x,y,z], 立方體在x、y、z三個維度上的長度.

center

false (默認值), 立方體位於第一卦限中(3個坐標軸正軸圍成的空間), 且一個角位於點(0,0,0)

true, 立方體的中心位於點(0,0,0)

默认值:  cube();   等效实现:  cube(size = [1, 1, 1], center = false);

示例:

本例的几种等效实现脚本
 cube(size = 18);
 cube(18);
 cube([18,18,18]);
 .
 cube(18,false);
 cube([18,18,18],false);
 cube([18,18,18],center=false);
 cube(size = [18,18,18], center = false);
 cube(center = false,size = [18,18,18] );

本例的几种等效实现脚本
 cube([18,28,8],true);
 box=[18,28,8];cube(box,true);

球體

在坐標系的原點處創建一個球體。參數名r可寫可不寫。若要以（直徑）d取代（半徑）r, 則必須寫參數名d。

參數

r: 半徑。此為球體的半徑。球體的分辨率基於球體的大小與$fa、$fs、$fn三個變量。至於這些特殊變量的更多信息請查閱: OpenSCAD用戶手冊/其他語言特性
d: 直徑。此為球體的直徑。
$fa: 以度數來表示的片段角度。
$fs: 以毫米（mm）表示的片段尺寸。
$fn: 分辨率

 默认值:  sphere();   等效实现:   sphere($fn = 0, $fa = 12, $fs = 2, r = 1);

用例

sphere(r = 1);
sphere(r = 5);
sphere(r = 10);
sphere(d = 2);
sphere(d = 10);
sphere(d = 20);

// 这将创建半径为2mm的高分辨率球体
sphere(2, $fn=100);

// 这同样将创建半径为2mm的高分辨率球体，
// 但是此球体的极点上却没有那么多的小三角形
sphere(2, $fa=5, $fs=0.1);

圓柱體

繞z軸創建一個圓柱體或一個圓錐體。當center為true時，它將垂直居中於z軸。

如果將參數按如下順序給出，則參數名可寫可不寫。如果填寫了其中一個參數名，那麼也要列出位於其後的參數名。

請注意: 如果要使用r, d, d1或d2，就一定要列出其參數名。

cylinder(h = height, r1 = BottomRadius, r2 = TopRadius, center = true/false);

參數

h : 圓柱體或圓錐體的高。

r : 圓柱體的半徑。r1 = r2 = r。

r1 : 圓錐體的底面半徑。

r2 : 圓錐體的頂面半徑。

d : 圓柱體的直徑。r1 = r2 = d / 2. [請注意: 需要使用版本 2014.03]

d1 : 圓錐體的底面直徑。r1 = d1 / 2. [請注意: 需要使用版本 2014.03]

d2 : 圓錐體的頂面直徑。r2 = d2 / 2. [請注意: 需要使用版本 2014.03]

center

false (默認值),z軸的取值範圍為0至h

true, z軸的取值範圍為-h/2至+h/2

$fa : 每個片段的最小角度(以角度來表示)。

$fs : 每個片段的最小圓周長度。

$fn : fixed number of fragments in 360 degrees. Values of 3 or more override $fa and $fs

$fa, $fs and $fn must be named. 點擊這裡來查閱更多細節。

默认值: cylinder();  等效实现: cylinder($fn = 0, $fa = 12, $fs = 2, h = 1, r1 = 1, r2 = 1, center = false);

等效脚本
 cylinder(h=15, r1=9.5, r2=19.5, center=false);
 cylinder(  15,    9.5,    19.5, false);
 cylinder(  15,    9.5,    19.5);
 cylinder(  15,    9.5, d2=39  );
 cylinder(  15, d1=19,  d2=39  );
 cylinder(  15, d1=19,  r2=19.5);

等效脚本
 cylinder(h=15, r1=10, r2=0, center=true);
 cylinder(  15,    10,    0,        true);
 cylinder(h=15, d1=20, d2=0, center=true);

center = false
center = true

等效脚本
 cylinder(h=20, r=10, center=true);
 cylinder(  20,   10, 10,true);
 cylinder(  20, d=20, center=true);
 cylinder(  20,r1=10, d2=20, center=true);
 cylinder(  20,r1=10, d2=2*10, center=true);

use of $fn

$fn值越大，創建的表面就越圓滑，當然，渲染花費的時間也就越長。在開發過程中為了渲染更快可取適中值，待最終渲染（F6）時再採用較大值。

然而，在取較小值時，卻會生成一些有意思的非圓形對象。以下幾個示例會演示這一點：

scripts for these examples
 cylinder(20,20,20,$fn=3);
 cylinder(20,20,00,$fn=4);
 cylinder(20,20,10,$fn=4);

undersized holes

When using cylinder() with difference() to place holes in objects, the holes will be undersized. This is because circular paths are approximated with polygons inscribed within in a circle. The points of the polygon are on the circle, but straight lines between are inside. To have all of the hole larger than the true circle, the polygon must lie wholly outside of the circle (circumscribed). Modules for circumscribed holes

精確度的相關注解 圓形對象都是以近似方式表示的。The algorithm for doing this matters when you want 3d printed holes to be the right size. Current behavior is illustrated in a diagram . Discussion regarding optionally changing this behavior happening in a Pull Request

多面體

多面體是一種最常用的3D圖元實體。可用它來創建任意具有凸凹（concave as well as convex）特性的規則或不規則形狀幾何體。而曲面則是由一系列平面近似構成。

polyhedron( points = [ [X₀, Y₀, Z₀], [X₁, Y₁, Z₁], ... ], triangles = [ [P₀, P₁, P₂], ... ], convexity = N);   // 2014.03版本以前
polyhedron( points = [ [X₀, Y₀, Z₀], [X₁, Y₁, Z₁], ... ], faces = [ [P₀, P₁, P₂, P₃, ...], ... ], convexity = N);   // 2014.03及其后续版本

參數

points

Vector of 3d points or vertices. Each point is in turn a vector, [x,y,z], of its coordinates.

Points may be defined in any order. N points are referenced, in the order defined, as 0 to N-1.

triangles [廢止: triangles 將從未來發行版中去掉。 Use faces parameter instead]

Template:Bookcat

Vector of faces which collectively enclose the solid. Each face is a vector containing the indices (0 based) of 3 points from the points vector.

faces [請注意: 需要使用版本 2014.03]

Vector of faces which collectively enclose the solid. Each face is a vector containing the indices (0 based) of 3 or more points from the points vector.

Faces may be defined in any order. Define enough faces to fully enclose the solid, with no overlap.

Points which describe a single face must all be on the same plane.

convexity

Integer. The convexity parameter specifies the maximum number of faces a ray intersecting the object might penetrate. This parameter is only needed for correctly displaying the object in OpenCSG preview mode. It has no effect on the polyhedron rendering. For display problems, setting it to 10 should work fine for most cases.

 默认值: polyhedron(); 等效实现: polyhedron(points = undef, faces = undef, convexity = 1);

All faces must have points ordered in the same direction . OpenSCAD prefers clockwise when looking at each face from outside inwards. The back is viewed from the back, the bottom from the bottom, etc..

示例1 利用多面體來生成立方體( [ 10, 7, 5 ] );

CubePoints = [
  [  0,  0,  0 ],  //0
  [ 10,  0,  0 ],  //1
  [ 10,  7,  0 ],  //2
  [  0,  7,  0 ],  //3
  [  0,  0,  5 ],  //4
  [ 10,  0,  5 ],  //5
  [ 10,  7,  5 ],  //6
  [  0,  7,  5 ]]; //7
  
CubeFaces = [
  [0,1,2,3],  // 底面
  [4,5,1,0],  // 前面
  [7,6,5,4],  // 顶面
  [5,6,2,1],  // 右面
  [6,7,3,2],  // 背面
  [7,4,0,3]]; // 左面
  
polyhedron( CubePoints, CubeFaces );

立方体底面的等价描述
  [0,1,2,3],
  [0,1,2,3,0],
  [1,2,3,0],
  [2,3,0,1],
  [3,0,1,2],
  // 两个未重叠的三角形
  [0,1,2],[2,3,0],   
  [1,2,3],[3,0,1],
  [1,2,3],[0,1,3],

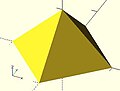
示例2 金字塔（以正方形為底座的錐體）：

polyhedron(
  points=[ [10,10,0],[10,-10,0],[-10,-10,0],[-10,10,0], // 底座上的4个顶点
           [0,0,10]  ],                                 // 锥体顶点 
  faces=[ [0,1,4],[1,2,4],[2,3,4],[3,0,4],              // 每个三角形面
              [1,0,3],[2,1,3] ]                         // 正方形底座上的两个三角形
 );

示例3 一個三稜柱:

   module prism(l, w, h){
       polyhedron(
               points=[[0,0,0], [l,0,0], [l,w,0], [0,w,0], [0,w,h], [l,w,h]],
               faces=[[0,1,2,3],[5,4,3,2],[0,4,5,1],[0,3,4],[5,2,1]]
               );
       
       // preview unfolded (do not include in your function
       z = 0.08;
       separation = 2;
       border = .2;
       translate([0,w+separation,0])
           cube([l,w,z]);
       translate([0,w+separation+w+border,0])
           cube([l,h,z]);
       translate([0,w+separation+w+border+h+border,0])
           cube([l,sqrt(w*w+h*h),z]);
       translate([l+border,w+separation+w+border+h+border,0])
           polyhedron(
                   points=[[0,0,0],[h,0,0],[0,sqrt(w*w+h*h),0], [0,0,z],[h,0,z],[0,sqrt(w*w+h*h),z]],
                   faces=[[0,1,2], [3,5,4], [0,3,4,1], [1,4,5,2], [2,5,3,0]]
                   );
       translate([0-border,w+separation+w+border+h+border,0])
           polyhedron(
                   points=[[0,0,0],[0-h,0,0],[0,sqrt(w*w+h*h),0], [0,0,z],[0-h,0,z],[0,sqrt(w*w+h*h),z]],
                   faces=[[1,0,2],[5,3,4],[0,1,4,3],[1,2,5,4],[2,0,3,5]]
                   );
       }
   
   prism(10, 5, 3);

Debugging polyhedra

Mistakes in defining polyhedra include not having all faces with the same order, overlap of faces and missing faces or portions of faces. As a general rule, the polyhedron faces should also satisfy (manifold conditions):

exactly two faces should meet at any polyhedron edge.
if two faces have a vertex in common, they should be in the same cycle face-edge around the vertex.

The first rule eliminates polyhedron like two cubes with a common edge and not watertight models; the second excludes polyhedron like two cubes with a common vertex.

When viewed from the outside, the points describing each face must be in the same order . OpenSCAD prefers CW, and provides a mechanism for detecting CCW. When the thrown together view (F12) is used with F5, CCW faces are shown in pink. Reorder the points for incorrect faces. Rotate the object to view all faces. The pink view can be turned off with F10.

OpenSCAD allows, temporarily, commenting out part of the face descriptions so that only the remaining faces are displayed. Use // to comment out the rest of the line. Use /* and */ to start and end a comment block. This can be part of a line or extend over several lines. Viewing only part of the faces can be helpful in determining the right points for an individual face. Note that a solid is not shown, only the faces. If using F12, all faces have one pink side. Commenting some faces helps also to show any internal face.

CubeFaces = [
/* [0,1,2,3],  // bottom
   [4,5,1,0],  // front */
   [7,6,5,4],  // top
/* [5,6,2,1],  // right
   [6,7,3,2],  // back */
   [7,4,0,3]]; // left

After defining a polyhedron, its preview may seem correct. The polyhedron alone may even render fine. However to be sure it is a valid manifold and that it will generate a valid STL file, union it with any cube and render it (F6). If the polyhedron disappears, it means that it is not correct. Revise the winding order of all faces and the two rules stated above.

Mis-ordered faces

Example 4 a more complex polyhedron with mis-ordered faces

When you select 'Thrown together' from the view menu and compile the design (not compile and render!) you will see a preview with the mis-oriented polygons highlighted. Unfortunately this highlighting is not possible in the OpenCSG preview mode because it would interfere with the way the OpenCSG preview mode is implemented.)

Below you can see the code and the picture of such a problematic polyhedron, the bad polygons (faces or compositions of faces) are in pink.

// Bad polyhedron
polyhedron
    (points = [
	       [0, -10, 60], [0, 10, 60], [0, 10, 0], [0, -10, 0], [60, -10, 60], [60, 10, 60], 
	       [10, -10, 50], [10, 10, 50], [10, 10, 30], [10, -10, 30], [30, -10, 50], [30, 10, 50]
	       ], 
     faces = [
		  [0,2,3],   [0,1,2],  [0,4,5],  [0,5,1],   [5,4,2],  [2,4,3],
                  [6,8,9],  [6,7,8],  [6,10,11], [6,11,7], [10,8,11],
		  [10,9,8], [0,3,9],  [9,0,6], [10,6, 0],  [0,4,10],
                  [3,9,10], [3,10,4], [1,7,11],  [1,11,5], [1,7,8],  
                  [1,8,2],  [2,8,11], [2,11,5]
		  ]
     );

A correct polyhedron would be the following:

polyhedron
    (points = [
	       [0, -10, 60], [0, 10, 60], [0, 10, 0], [0, -10, 0], [60, -10, 60], [60, 10, 60], 
	       [10, -10, 50], [10, 10, 50], [10, 10, 30], [10, -10, 30], [30, -10, 50], [30, 10, 50]
	       ], 
     faces = [
		  [0,3,2],  [0,2,1],  [4,0,5],  [5,0,1],  [5,2,4],  [4,2,3],
                  [6,8,9],  [6,7,8],  [6,10,11],[6,11,7], [10,8,11],
		  [10,9,8], [3,0,9],  [9,0,6],  [10,6, 0],[0,4,10],
                  [3,9,10], [3,10,4], [1,7,11], [1,11,5], [1,8,7],  
                  [2,8,1],  [8,2,11], [5,11,2]
		  ]
     );

Beginner's tip:

If you don't really understand "orientation", try to identify the mis-oriented pink faces and then invert the sequence of the references to the points vectors until you get it right. E.g. in the above example, the third triangle ([0,4,5]) was wrong and we fixed it as [4,0,5]. Remember that a face list is a circular list. In addition, you may select "Show Edges" from the "View Menu", print a screen capture and number both the points and the faces. In our example, the points are annotated in black and the faces in blue. Turn the object around and make a second copy from the back if needed. This way you can keep track.

Clockwise Technique:

Orientation is determined by clockwise circular indexing. This means that if you're looking at the triangle (in this case [4,0,5]) from the outside you'll see that the path is clockwise around the center of the face. The winding order [4,0,5] is clockwise and therefore good. The winding order [0,4,5] is counter-clockwise and therefore bad. Likewise, any other clockwise order of [4,0,5] works: [5,4,0] & [0,5,4] are good too. If you use the clockwise technique, you'll always have your faces outside (outside of OpenSCAD, other programs do use counter-clockwise as the outside though).

Think of it as a Left Hand Rule:

If you hold the face and the fingers of your right hand curls is the same order as the points, then your thumb points outwards.

Succinct description of a 'Polyhedron'

* Points define all of the points/vertices in the shape.
* Faces is a list of flat polygons that connect up the points/vertices.

Each point, in the point list, is defined with a 3-tuple x,y,z position specification. Points in the point list are automatically enumerated starting from zero for use in the faces list (0,1,2,3,... etc).

Each face, in the faces list, is defined by selecting 3 or more of the points (using the point order number) out of the point list.

e.g. faces=[ [0,1,2] ] defines a triangle from the first point (points are zero referenced) to the second point and then to the third point.

When looking at any face from the outside, the face must list all points in a clockwise order.

Point repetitions in a polyhedron point list

The point list of the polyhedron definition may have repetitions. When two or more points have the same coordinates they are considered the same polyhedron vertex. So, the following polyhedron:

points = [[ 0, 0, 0], [10, 0, 0], [ 0,10, 0],
          [ 0, 0, 0], [10, 0, 0], [ 0,10, 0],
          [ 0,10, 0], [10, 0, 0], [ 0, 0,10],
          [ 0, 0, 0], [ 0, 0,10], [10, 0, 0],
          [ 0, 0, 0], [ 0,10, 0], [ 0, 0,10]];
polyhedron(points, [[0,1,2], [3,4,5], [6,7,8], [9,10,11], [12,13,14]]);

define the same tetrahedron as:

points = [[0,0,0], [0,10,0], [10,0,0], [0,0,10]];
polyhedron(points, [[0,2,1], [0,1,3], [1,2,3], [0,3,2]]);