初中數學/畢氏定理
外观
< 初中數學
畢氏定理
[编辑]直角三角形,長股平方+短股平方=斜邊平方,一般表達為:
a2+b2=c2
面積公式
[编辑]- 長方形面積=長×寬
- 三角形面積=底×高/2
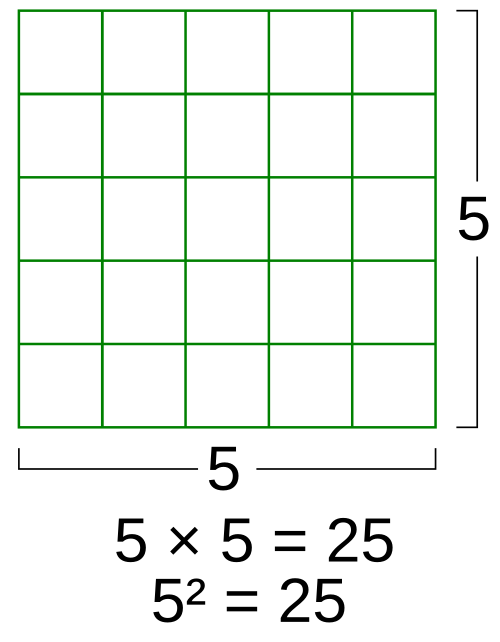
- 正方形面積=邊長×邊長
平方
[编辑]直角三角形
[编辑]
三角形三個角當中有一個角是直角,這個三角形就叫做直角三角形。
直角的對邊叫做「斜邊」,直角的兩個鄰邊叫做「股」。
右方直角三角形,C為直角,另兩角為A、B,a為短股、b為長股、c為斜邊。
圖形重新排列證明畢氏定理
[编辑]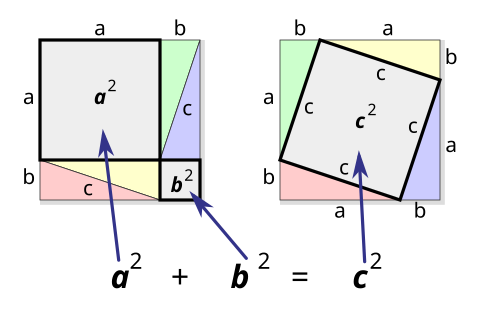
圖中,左右兩個大的正方形的邊長都是 a + b ,同時,兩個大正方形的內部都有四個面積一模一樣的直角三角形(邊長都是 a、b、c ),只是兩邊的排列方式不一樣而已。
兩個大正方形的面積皆為(a+b)2。把四個相等的三角形移除後,左方餘下面積為a2+b2,右方餘下面積為c2,兩者相等。
加法平方公式
[编辑]由上圖也可以表示出「加法平方公式」
(a+b)2=a2+2×a×b+b2