首页 > 維基書架 > 数学书架 > 算术
以下習題另有解答,但強烈建議先練習習題,才看解答校正錯誤,而不是先偷看解答。
- O → 1個O
- OO → 2個O
- OOO → 3個O
- OOOO → 4個O
- OOOOO → 5個O
- OOOOOO → 6個O
- OOOOOOO → 7個O
- OOOOOOOO → 8個O
- OOOOOOOOO → 9個O
- OOOOOOOOOO → 10個O
 習題:
習題:
- 以下的圖形共有幾個O?
- OOOOO → ?個O
- OOO → ?個O
- OOOOOOOO → ?個O
- O → ?個O
- OOOOOO → ?個O
- 試畫出指定個數的O:
- 4个O
- 2个O
- 7个O
- 10个O
- 9个O
哪邊的O比較多?
1. OOOOOOOO、OOOOO
2. OOOO、OOOOOOOOO
3. OOOOOOOOOO、OOOOOOO
4. OOOOO、OOOOOO
假設有兩個數字,若該數字代表的O比較多,則該數字比較大。
大於、小於符號分別以“ ”、“
”、“ ”表示,開口一邊的數字比較大,若
”表示,開口一邊的數字比較大,若 則稱A小於B,若
則稱A小於B,若 則稱A大於B。
則稱A大於B。
例子:
 →
→  → 4大於1
→ 4大於1
 →
→  → 2小於5
→ 2小於5
 →
→  → 6大於4
→ 6大於4
 →
→  → 7小於8
→ 7小於8
加法的符號是「 」,讀作「加號」,加號前的數稱為「被加數」,加號後的數是「加數」,等號後面的答案稱為「和」,如下例題:
」,讀作「加號」,加號前的數稱為「被加數」,加號後的數是「加數」,等號後面的答案稱為「和」,如下例題:


1是被加數,它被「加上」某個特定的數值1,也就是加數,得到和2。
 習題:
習題:
 ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
?
減法的符號是「 」,讀作「減號」,減號前的數稱為「被減數」,減號後的數是「減數」,等號後面的答案稱為「差」,如例題:
」,讀作「減號」,減號前的數稱為「被減數」,減號後的數是「減數」,等號後面的答案稱為「差」,如例題:
36是被減數,從这个数中被「減掉」11;导致别的数的数值减少的数就是減數(此例中的11)。36被11減,得到差25。
如果被减数小于减数,就會出現負數。如:

減法也是加法的逆算,若將減數加上差可得被減數,就拿上面的例子來說明:
 ,其中36是被減數,11是減數,25是差。
,其中36是被減數,11是減數,25是差。

將減數11加給25,即 得到原来的被减数。
得到原来的被减数。
另外以下是退位減法的計算方式:
例如:238-74=?
我們可列豎式計算:

先計算個位數的部份:8-4=4
所以個位數先寫上4。

十位數不夠減,可以向百位數拿個1過來,變成13-7,運用口訣-7=-10+3,13-10+3=6,所以十位數先寫上6。

因為我們已經從百位數的2拿1走了,所以百位數剩下1。

所以得到的解:238-74=164
 習題:
習題:
 ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
?
乘法的符號是「 」或「
」或「 」,在電腦上常以「
」,在電腦上常以「 」表示,讀作「乘號」,乘號前的數稱為「被乘數」,乘號後的數是「乘數」,等號後面的答案稱為「積」,如例題:
」表示,讀作「乘號」,乘號前的數稱為「被乘數」,乘號後的數是「乘數」,等號後面的答案稱為「積」,如例題: 。若乘數及被乘數是10或以下,那麼我們便要依賴乘法表來計算。此外,也可於被乘數或乘數加上括號去代替乘號,如例題:
。若乘數及被乘數是10或以下,那麼我們便要依賴乘法表來計算。此外,也可於被乘數或乘數加上括號去代替乘號,如例題: 。
。
附錄的#乘法表,被乘數是1時,不必背誦。背誦其他九九乘法的積時,由簡至難的被乘數順序一般認爲是2、5、4、8、3、6、9、7。
乘法的法則:
- 交換律:

- 結合律:

- 分配律:



 習題:
習題:
 ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
?
除法的符號是「 」,或以分線表示,在電腦上常以「
」,或以分線表示,在電腦上常以「 」表示,它們均讀作「除號」,除號前的數稱為「被除數」,除號後的數是「除數」,等號後面的答案稱為「商」,如例題:
」表示,它們均讀作「除號」,除號前的數稱為「被除數」,除號後的數是「除數」,等號後面的答案稱為「商」,如例題: 。若除數及被除數是10或以下,那麼我們便要依賴乘法表來計算。另外,部分數被除後可能出現循環小數或無限小數,那麼便需要轉化成分數來表示(有關小數和分數的資料,將會在下章介紹)。
。若除數及被除數是10或以下,那麼我們便要依賴乘法表來計算。另外,部分數被除後可能出現循環小數或無限小數,那麼便需要轉化成分數來表示(有關小數和分數的資料,將會在下章介紹)。
另外,除的意義為「將一份平均地分為多份」,因此所有數除以零是無效(meaningless)的。
除法可以解讀成「重複的減法」。
例如 : ,就好像
,就好像 ,
, ,
, 被
被 減了兩次就變成
減了兩次就變成
 = ?
= ?



 ,因值已經低於0了,不能採用!
,因值已經低於0了,不能採用!
 被
被 連減了3次,
連減了3次, 就是餘數。所以
就是餘數。所以 = 3餘3
= 3餘3
除法的法則:

 (
( ≠
≠ )
) = ∞,無窮大
= ∞,無窮大 = 不定值
= 不定值 = 負無限
= 負無限
 習題:
習題:
 ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
? ?
?
 等同於
等同於 自乘
自乘  次,即
次,即 。
。
- 主页面:算术/开方
开方是乘方的逆运算。
所谓四则运算,是指数与数之间的加、减、乘、除这四种基本运算。括號 之内的部份要先計算,然後四則運算要先乘除後加減。
之内的部份要先計算,然後四則運算要先乘除後加減。
例题:
上題為:


 在此步看見
在此步看見 與
與 可以把他們相約 改寫為
可以把他們相約 改寫為 也稱跳步
也稱跳步


 習題:
習題:
 ?
? ?
? ?
? ?
?![{\displaystyle 36+[(36+5)\times 2-11\times 7]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee652ced36702f0e596f5b2e6fa39d94bc4ae969) ?
?
- 小數就是整數和整數之間的數。整數和小數之間會有一個點,稱為「小數點」。例:3.5 ,4.5 ,8.45.
- 分數類似小數,表示方式是在兩個數字之間加上一條線。通常下面是分母,代表共有多少份。上面是分子,也就是佔多少份。例:5/3
 習題:
習題:
請分辨出分數和小數.
- 3.5
- 2/5
- 6.7
- 5/3
- 10/13
- 4.7
百分率亦類似小數,表示的方法是在一個數字後加上百分比符號"%"。100%亦等於1。百分率的用途有很多,有計算機率、表示數量等,例:35%, 48%.
注意:"%"的意思是百分之一,並不是除以100。
自古以来,人们总结了很多速算技巧。利用这些技巧,在很多情况下,能够极大地提高人们的计算速度。
- 兩數交叉型減法速解法:
- 例如:
 (由6和3所組成的算式,6用3去減,再乘以9)。
(由6和3所組成的算式,6用3去減,再乘以9)。
- 10的n次方减某数:
 ,速算法為将
,速算法為将 视为
视为 ,并分拆各数位(
,并分拆各数位( ),然后各数位相减(
),然后各数位相减( ),得出最终结果(
),得出最终结果( )。
)。
- 乘以5的数:
- 数字乘以5:
 ,速算法為將36乘以10(
,速算法為將36乘以10( ),再将结果除以2(
),再将结果除以2( )。
)。
- 乘以11的數:
- 兩位數乘以11:
 ,速算法為將6、3兩數之和(
,速算法為將6、3兩數之和( ),插入36的中間,(如和超過10則進位),即
),插入36的中間,(如和超過10則進位),即 。
。
- 三位數乘以11:
 ,速算法為將
,速算法為將 、
、 插入5、6的中間,即
插入5、6的中間,即 。
。
- 四位數乘以11:
 ,速算法為將
,速算法為將 拆成
拆成 ,再用
,再用 去乘它們,又
去乘它們,又 ,
, ,故
,故 。
。
 ,速算法為將
,速算法為將 拆成
拆成 ,再用
,再用 去乘它們,又
去乘它們,又 ,
, ,故
,故 。
。
- 乘以111的數:
- 兩位數乘以111:
 ,速算法為將6、3兩數之和
,速算法為將6、3兩數之和 ,加兩次,插入36的中間,(如和超過10則進位),即
,加兩次,插入36的中間,(如和超過10則進位),即 。
。
- 三位數乘以111:
 ,速算法為將
,速算法為將 拆成
拆成 ,再用
,再用 去乘它們,又
去乘它們,又 ,
, ,故
,故 。
。
- 兩位數乘以121:
 ,速算法為將
,速算法為將 拆為
拆為 。
。
- 主页面:w:格子乘法
第一步:画带斜线的格子,将第一数(58)写在格子顶部,第二数(213)书写着格子的右侧如图,格子斜线下方写下乘积的个位数,格子斜线之上写入乘积的十位数。
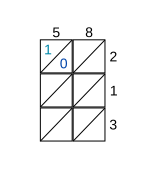 第一步
第一步
第二步:将每个格子顶上数字与同一格子右边的数字相乘,将乘积逐个写入格子内,然后自下而上按斜线将数字相加,将所得的和写在格子图之下或左边:
 ,将4写在斜线对齐的格子图下边。
,将4写在斜线对齐的格子图下边。 ,将和的个位数“5”写在斜线对齐的格子下边,十位数进位到下一位斜线中如图
,将和的个位数“5”写在斜线对齐的格子下边,十位数进位到下一位斜线中如图 ,将和的个位数写在斜线对齐的格子边上(左边),将十位数进位。
,将和的个位数写在斜线对齐的格子边上(左边),将十位数进位。 ,记入格子左边
,记入格子左边
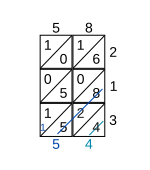 第二步
第二步
第三步:从格子左边自上而下,接格子下边自左至右,读出乘积:12354
所以 
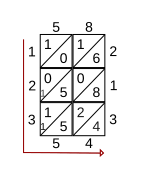 第三步
第三步
- 除以5的数:
- 数字除以5:
 ,速算法為將36除以10(
,速算法為將36除以10( ),再将结果乘以2(
),再将结果乘以2( )。
)。
- 除以11的数:
- 数字除以11:
 ,速算法为从左侧依序删除数字,并记录删除的数字,然后再在下一个数位减去删除的数字。
,速算法为从左侧依序删除数字,并记录删除的数字,然后再在下一个数位减去删除的数字。
 从左侧删除一位数字之后为
从左侧删除一位数字之后为 ,记录
,记录 。
。 。
。 从左侧删除一位数字之后为
从左侧删除一位数字之后为 ,记录
,记录 。
。 。
。 从左侧删除一位数字之后为
从左侧删除一位数字之后为 ,记录
,记录 。
。 。
。 从左侧删除一位数字之后为
从左侧删除一位数字之后为 ,记录
,记录 。
。 。
。- 最后将从左侧依序删除的数字按照数位顺序串联成一个完整的数字:
 。
。
- 下方为遇到特殊情况时的处理方式:
 。
。
 从左侧删除一位数字之后为
从左侧删除一位数字之后为 ,记录
,记录 。
。- 但
 的结果为负数:此时将将原先记录的数字减1,改记录
的结果为负数:此时将将原先记录的数字减1,改记录 ;然后将减数的首数位减一,并在被减数的首数位前添加数位1,得
;然后将减数的首数位减一,并在被减数的首数位前添加数位1,得 。
。
- 但此时结果的前两位数字为
 ,无法进行下一步行动,否则会陷入死循环。此时应该将
,无法进行下一步行动,否则会陷入死循环。此时应该将 视为一个独立的数位整体,然后执行下一步行动。
视为一个独立的数位整体,然后执行下一步行动。
 从左侧删除(技术上的)一位数字之后为
从左侧删除(技术上的)一位数字之后为 ,记录
,记录 。
。 的结果为负数。
的结果为负数。- 此时将原先记录的数字减1,改记录
 。然后将减数的(技术上的)首数位减一,并在被减数的首数位前添加数位1,得
。然后将减数的(技术上的)首数位减一,并在被减数的首数位前添加数位1,得 。
。
 从左侧删除一位数字之后为
从左侧删除一位数字之后为 ,记录
,记录 。
。 。
。- 最后将从左侧依序删除的数字按照数位顺序串联成一个完整的数字:
 。
。
7是很特殊的数字,而求除以7的小数值往往令人头疼。其实除以7的计算中蕴藏着非常简单的规律。请看:






看出规律没有? ,后面的数刚好是前面的两倍,
,后面的数刚好是前面的两倍, ,而
,而 刚好进一位就成57,后面
刚好进一位就成57,后面 ,
, ,
, ,
, ,
, 正好都是这串數中的一段,只是起始位置不同而已。只要记住142857这串數,就可以很易算出所有除以7的值。
正好都是这串數中的一段,只是起始位置不同而已。只要记住142857这串數,就可以很易算出所有除以7的值。
高中化学有條定理,这规律非常有用:1摩任何气体的体积都接近22.4升。而 ,
, ,在计算中,3.2这因子很易约去,而知道除以7的规律,这种计算往往就变得很快。
,在计算中,3.2这因子很易约去,而知道除以7的规律,这种计算往往就变得很快。
建议阁下在阅读此节前先阅读并熟记
§ 乘方表一节的内容。
- 10至19的乘方:

- 20至99的乘方:
- 同前式,但须将20至99之间的数取近似值至十位,并将原式中的10替换成此数。
公式可以將繁複的計算變易。
- 分配率:

- 和平方:

- 三數和平方:

- 差平方:

- 平方差:

- 和立方:

- 差立方:

- 立方和:

- 立方差:








 已知
已知 ,求a的值。
,求a的值。
解答:

| +
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| 2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
| 3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
| 4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
| 5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
| 6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
| 7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
| 8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
| 9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
| ×
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
| 1
|
1
|
|
|
|
|
|
|
|
|
| 2
|
2
|
4
|
|
|
|
|
|
|
|
| 3
|
3
|
6
|
9
|
|
|
|
|
|
|
| 4
|
4
|
8
|
12
|
16
|
|
|
|
|
|
| 5
|
5
|
10
|
15
|
20
|
25
|
|
|
|
|
| 6
|
6
|
12
|
18
|
24
|
30
|
36
|
|
|
|
| 7
|
7
|
14
|
21
|
28
|
35
|
42
|
49
|
|
|
| 8
|
8
|
16
|
24
|
32
|
40
|
48
|
56
|
64
|
|
| 9
|
9
|
18
|
27
|
36
|
45
|
54
|
63
|
72
|
81
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
| ^
|
2
|
3
|
| 1
|
1
|
1
|
| 2
|
4
|
8
|
| 3
|
9
|
27
|
| 4
|
16
|
64
|
| 5
|
25
|
125
|
| 6
|
36
|
216
|
| 7
|
49
|
343
|
| 8
|
64
|
512
|
| 9
|
81
|
729
|
| log
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
| 10
|
0000
|
0043
|
0086
|
0128
|
0170
|
0212
|
0253
|
0294
|
0334
|
0374
|
| 11
|
0414
|
0453
|
0492
|
0531
|
0569
|
0607
|
0645
|
0682
|
0719
|
0755
|
| 12
|
0792
|
0828
|
0864
|
0899
|
0934
|
0969
|
1004
|
1038
|
1072
|
1106
|
| 13
|
1139
|
1173
|
1206
|
1239
|
1271
|
1303
|
1335
|
1367
|
1399
|
1430
|
| 14
|
1461
|
1492
|
1523
|
1553
|
1584
|
1614
|
1644
|
1673
|
1703
|
1732
|
| 15
|
1761
|
1790
|
1818
|
1847
|
1875
|
1903
|
1931
|
1959
|
1987
|
2014
|
| 16
|
2041
|
2068
|
2095
|
2122
|
2148
|
2175
|
2201
|
2227
|
2253
|
2279
|
| 17
|
2304
|
2330
|
2355
|
2380
|
2405
|
2430
|
2455
|
2480
|
2504
|
2529
|
| 18
|
2553
|
2577
|
2601
|
2625
|
2648
|
2672
|
2695
|
2718
|
2742
|
2765
|
| 19
|
2788
|
2810
|
2833
|
2856
|
2878
|
2900
|
2923
|
2945
|
2967
|
2989
|
| 20
|
3010
|
3032
|
3054
|
3075
|
3096
|
3118
|
3139
|
3160
|
3181
|
3201
|
| 21
|
3222
|
3243
|
3263
|
3284
|
3304
|
3324
|
3345
|
3365
|
3385
|
3404
|
| 22
|
3424
|
3444
|
3464
|
3483
|
3502
|
3522
|
3541
|
3560
|
3579
|
3598
|
| 23
|
3617
|
3636
|
3655
|
3674
|
3692
|
3711
|
3729
|
3747
|
3766
|
3784
|
| 24
|
3802
|
3820
|
3838
|
3856
|
3874
|
3892
|
3909
|
3927
|
3945
|
3962
|
| 25
|
3979
|
3997
|
4014
|
4031
|
4048
|
4065
|
4082
|
4099
|
4116
|
4133
|
| 26
|
4150
|
4166
|
4183
|
4200
|
4216
|
4232
|
4249
|
4265
|
4281
|
4298
|
| 27
|
4314
|
4330
|
4346
|
4362
|
4378
|
4393
|
4409
|
4425
|
4440
|
4456
|
| 28
|
4472
|
4487
|
4502
|
4518
|
4533
|
4548
|
4561
|
4579
|
4594
|
4609
|
| 29
|
4624
|
4639
|
4654
|
4669
|
4683
|
4698
|
4713
|
4728
|
4742
|
4757
|
| 30
|
4771
|
4786
|
4800
|
4814
|
4829
|
4843
|
4857
|
4871
|
4886
|
4900
|
| 1
|
0
|
| 2
|
0.693147180559945
|
| 3
|
1.09861228866811
|
| 4
|
1.386294361119891
|
| 5
|
1.6094379124341
|
| 6
|
1.791759469228055
|
| 7
|
1.945910149055313
|
| 8
|
2.079441541679836
|
| 9
|
2.19722457733622
|
| 10
|
2.302585092994046
|
| 11
|
2.397895272798371
|
| 12
|
2.484906649788
|
| 13
|
2.564949357461537
|
| 14
|
2.639057329615258
|
| 15
|
2.70805020110221
|
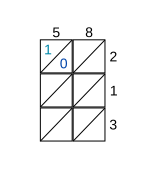








































































































































![{\displaystyle 36+[(36+5)\times 2-11\times 7]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee652ced36702f0e596f5b2e6fa39d94bc4ae969)


















































































































