国中数学/国中数学七年级/8-1 垂直与线对称
| 7-3 一元一次不等式的应用问题 | ◄ | 国中数学七年级 8-1 垂直与线对称 |
► | 8-2 三视图 |
本单元为国中阶段第一次的几何课程,我们将从最简单的几何图形开始介绍。
几何图形
[编辑]点
[编辑]点(point)是最基本的几何图形,一个点只代表位置,它不具有大小与长度。
点的命名
[编辑]通常我们会使用大写英文字母、、、、等标示点,并称呼为“什么点”或“点什么”。
Example:用大写字母标示的点我们称为点或点。(如下图所示)
线
[编辑]任意两点就可以决定唯一的一条直线。(这是欧几里得几何公理之一,有兴趣的同学可以点入连结参看。)
- 直线
- 两端可以无限延长的线我们称作直线。
- 直线没有长度和宽度,也没有方向性。
- 直线的命名:除非要特别说明这条直线过两点与我们记录成之外,其余大部分都是在直线旁边标示大写英文字母、、等符号,若需要表示更多直线就会在大写英文字母左下方写上小小的数字(称为下标),形如、、……等等。
- 点在直线上代表直线会通过点。
- 若与为任意两点,则与这两个直线的表达方式代表相同的直线。
- 线段
- 两端都不可以延伸的线我们称作线段。
- 线段具有长度,但没有宽度与方向性。
- 线段的命名:通过两点与的线段我们可以记录成或,其中读作“线段”或“线段”。
- 因为线段具有长度,故有时会表示线段的长度。如的长度为厘米,我们可以写作厘米。
- 线段可以比大小:
- 若比长,代表将点与点重合之后,点会介于、两点之间,此时我们可以写作。
- 若比短,代表将点与点重合之后,点会落在之外,此时我们可以写作。
- 若比等长,代表将点与点重合之后,点会与点重合,此时我们可以写作。
- 点在上代表会通过点。
- 射线
- 只有一端可以无限延长的线我们称作射线。
- 射线具有方向性,但没有长度与宽度。
- 线段的命名:若点不可无限延伸,但点可以,我们将此射线记录成,读作“射线”或“射线”。
- 注意:不可以纪录为,因为这代表点可以无限延伸,但点不可。
- 由此可知并不等于。
- 点在上代表会通过点。
角
[编辑]参见:国中数学/国中数学八年级/8-1 角
两射线如果使用相同的起点,则会形成一个角,此起点我们称为角的顶点。
| 角的种类 | |
|---|---|
| 锐角 | 介于0度到90度的角 |
| 直角 | 等于90度的角 |
| 钝角 | 介于90度到180度的角 |
| 平角 | 等于180度的角 |
| 优角 | 介于180度到360度的角 |
| 周角 | 等于360度的角 |
角的命名
[编辑]
- 可以直接在角上面标示、、、、……,并称呼为“(读作角)”、“”、“”、“”等等。
- 在不会造成混淆的情况下,可以标示出顶点,并利用顶点命名。例如有一个角的顶点为,我们称此角为。
- 若有可能造成混淆,可以在两射线上各取一点,并以顺时针或逆时针的方式报读角的名字。如右图为(顺时针)或(逆时针)[注 1],但不可以称或(即顶点必须在中间)。
- 下图为一个可能会造成混淆的例子:
 |
|---|
- 如果只是说,不知道是要表达、还是。
- 如果要表示最大的那个角,应该要用来说明比较好。
三角形
[编辑]由三个点用线段互相连起来的图形,我们称为三角形。三角形具有条边、个角与个顶点。是中学时期学习最多的形状。
- 依内角的大小可以将三角形区分成三类:
| 锐角三角形 | 三个内角都是锐角 |
| 直角三角形 | 三个内角当中有一个直角 |
| 钝角三角形 | 三个内角当中有一个钝角 |
- 其中,依边的长短可以分出特别的两类三角形:
| 等腰三角形 | 其中两条边等长 |
| 正三角形 | 三条边都等长 |
三角形的命名
[编辑]三角形的命名如同角的命名,可以顺时针报读或逆时针报读,但它跟角报读方式的不同之处在于三角形可以从任何点开始。如下图,你可以称下面这个三角形为、、、、、。
但在大部分的情形[注 2]我们会习惯将英文字母按照顺序排列,记作,读作“三角形”,很少人称作“三角形”。
多边形
[编辑]由个点以上(含),相邻的两点以线段连成一圈的图形,我们称为多边形。
- 一个边形有个顶点、条边与个角。
- 三角形也是一种多边形。
- 国中阶段会比较著墨在三角形、四边形与正多边形上。
- 多边形的称呼:从某一个顶点出发,依序以顺时针或逆时针的顺序报读各顶点。一样的,习惯上我们会按照英文字母的顺序报读。
 |
| 此四边形可以称呼它为四边形或四边形等等,但不能称呼为四边形。 |
- 多边形的对角线:不相邻的两点连成的线,我们称为对角线。
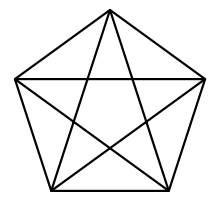
图中画出五边形所有的对角线。 - 补充:边形的对角线有个顶点。
- 若对角线全部都在图形之内,我们称此图形为凸多边形,若有一条对角线的部分会在图形之外,则我们称此图形为凹多边形。
- 在国中数学内,没有特别强调时,谈论的图形都是凸多边形。
 |
 |
圆
[编辑]参见:国中数学/国中数学九年级/2-1 点、线、圆
在平面上,与一固定点距离相同的所有点形成的图形,我们称为圆,其中“相同的距离”我们称为半径。
垂直
[编辑]当两直线(或线段)的夹角刚好是直角时,我们称两直线(或线段)垂直,并使用“”表示。如下图直线与直线垂直,我们可以写作“”。
 |
垂线
[编辑]垂线:一直线与直线的夹角为直角(两直线互相垂直),则我们称此直线为垂线。
1.一条直线的垂线有无限多条。
- 如下图当中,、与都是的垂线。
- 当然,只要在画一条直线,其夹角与直线成度的时候,这条直线也会是直线的垂线。
 |
2.过线上一点作的垂线只有一条。
- 如上图当中,过点且与垂直的直线只有一条。
3.过线外一点作的垂线只有一条。
垂足
[编辑]两垂直的直线(或线段)所相交的点,我们称为垂足。如上图当中的、、三点,分别是直线与、、的垂足。
平分
[编辑]设一线段,若点在上且满足,则我们称点平分,点也称作、两点的中点。

垂直平分线(中垂线)
[编辑]若点平分,则过点且与垂直的直线我们称为的垂直平分线,又称作中垂线。
- 只有线段才有垂直平分线,直线与射线没有。
- 一条线段的垂直平分线只有一条。
线对称图形
[编辑]- 线对称图形的意义:将一个平面图形沿着某一条直线对折,如果可以使直线两侧的图形完全重叠,则此图形为线对称图形。

一些线对称图形,红色直线为对称轴。 - 对称轴:在线对称图形中,若沿着直线对折,直线两侧的图形完全重叠,则直线称为线对称图形的对称轴。

- 注解:
- 在线对称图形中,对称轴为两侧对称点连线的垂直平分线。
- 如上图当中,直线为的垂直平分线。
- 在线对称图形中,对称线段等长,对称角等大。
- 如上图当中的对应边为,所以、的对应角为,所以。
- 在线对称图形中,对称轴为两侧对称点连线的垂直平分线。
常见的线对称图形
[编辑]- 等腰三角形
- 等腰三角形的定义:有两条边相等的三角形。
- 一般的等腰三角形只有一条对称轴,此对称轴既是底边的垂直平分线,也会将顶角平分成两个角度相等的角(我们称作角平分线)。
- 等腰三角形的两个底角相等。
- 正三角形
- 正三角形必定有条对称轴。
- 正三角形必然是等腰三角形,但等腰三角形不一定是正三角形。
- 长方形
- 长方形的定义:有四个直角的四边形。
- 一般的长方形有条对称轴。
- 菱形
- 菱形的定义:有四边等长的四边形。
- 一般的菱形有条对称轴。
- 正方形
- 正方形的定义:四边等长、四个角都是直角的四边形。
- 正方形必定有条对称轴。
- 正方形必然是长方形,但长方形不一定是正方形。
- 正方形必然是菱形,但菱形不一定是正方形。
- 筝形
- 筝形的定义:有两对邻边相等的四边形。
- 筝形又称作鸢形。
- 一般的筝形只有一条对称轴。
- 正方形、菱形必然是筝形,但筝形不一定是正方形或菱形。
- 等腰梯形
- 等腰梯形的意义:一个梯形的两腰等长。
- 等腰梯形只有一条对称轴。
- 正多边形
- 正多边形的对称轴和它的边数一样多。如正七边形有七条对称轴。
- 圆形
- 圆形有无限多条对称轴,任何一条直径都是其对称轴。
常考的"非"线对称图形
[编辑]- 内角分别是度的三角形。
- 一般的平行四边形。
- 一般的梯形。
剪纸与线对称图形
[编辑]将一张纸对折,并在折线画图案,剪下来的图形必定以折线作为其对称轴。
方格纸与线对称图形
[编辑]其秘诀为:对称点与对称轴的距离相等,利用方格纸上的格子可以测量距离,找出对称点然后再相连即可。











































































