國中數學/國中數學七年級/8-1 垂直與線對稱

7-3 一元一次不等式的應用問題

◄

國中數學七年級 8-1 垂直與線對稱

►

8-2 三視圖

本單元為國中階段第一次的幾何課程，我們將從最簡單的幾何圖形開始介紹。

幾何圖形

點

點(point)是最基本的幾何圖形，一個點只代表位置，它不具有大小與長度。

點的命名

通常我們會使用大寫英文字母$A$、$B$、$C$、$P$、$Q$等標示點，並稱呼為「什麼點」或「點什麼」。
Example：用大寫字母$A$標示的點我們稱為$A$點或點$A$。(如下圖所示)

線

任意兩點就可以決定唯一的一條直線。(這是歐幾里得幾何公理之一，有興趣的同學可以點入連結參看。)

1. 直線
   • 兩端可以無限延長的線我們稱作直線。
   • 直線沒有長度和寬度，也沒有方向性。
   • 直線的命名：除非要特別說明這條直線過兩點$A$與$B$我們記錄成${\overleftrightarrow {AB}}$之外，其餘大部分都是在直線旁邊標示大寫英文字母$L$、$M$、$N$等符號，若需要表示更多直線就會在大寫英文字母$L$左下方寫上小小的數字（稱為下標），形如$L_{1}$、$L_{2}$、$L_{3}$……等等。
   • 點$P$在直線$L$上代表直線${\color {red}L}$會通過${\color {red}P}$點。
   • 若$A$與$B$為任意兩點，則${\overleftrightarrow {AB}}$與${\overleftrightarrow {BA}}$這兩個直線的表達方式代表相同的直線。
2. 線段
   • 兩端都不可以延伸的線我們稱作線段。
   • 線段具有長度，但沒有寬度與方向性。
   • 線段的命名：通過兩點$A$與$B$的線段我們可以記錄成${\overline {AB}}$或${\overline {BA}}$，其中${\overline {AB}}$讀作「線段$AB$」或「$AB$線段」。
   • 因為線段具有長度，故有時${\overline {AB}}$會表示線段的長度。如${\overline {AB}}$的長度為$5$公分，我們可以寫作${\overline {AB}}=5$公分。
   • 線段可以比大小：
     1. 若${\overline {AB}}$比${\overline {CD}}$長，代表將$A$點與$C$點重合之後，$D$點會介於$A$、$B$兩點之間，此時我們可以寫作${\overline {AB}}>{\overline {CD}}$。
     2. 若${\overline {AB}}$比${\overline {CD}}$短，代表將$A$點與$C$點重合之後，$D$點會落在${\overline {AB}}$之外，此時我們可以寫作${\overline {AB}}<{\overline {CD}}$。
     3. 若${\overline {AB}}$比${\overline {CD}}$等長，代表將$A$點與$C$點重合之後，$D$點會與$B$點重合，此時我們可以寫作${\overline {AB}}={\overline {CD}}$。
   • 點$P$在${\overline {AB}}$上代表${\color {red}{\overline {AB}}}$會通過${\color {red}P}$點。
3. 射線
   • 只有一端可以無限延長的線我們稱作射線。
   • 射線具有方向性，但沒有長度與寬度。
   • 線段的命名：若$A$點不可無限延伸，但$B$點可以，我們將此射線記錄成${\overrightarrow {AB}}$，讀作「射線$AB$」或「$AB$射線」。
     • 注意：不可以紀錄為${\overrightarrow {BA}}$，因為這代表$A$點可以無限延伸，但$B$點不可。
     • 由此可知${\overrightarrow {AB}}$並不等於${\overrightarrow {BA}}$。
   • 點$P$在${\overrightarrow {AB}}$上代表${\color {red}{\overrightarrow {AB}}}$會通過${\color {red}P}$點。

角

參見：國中數學/國中數學八年級/8-1 角
兩射線如果使用相同的起點，則會形成一個角，此起點我們稱為角的頂點。

角的種類	定義
銳角	介於0度到90度的角
直角	等於90度的角
鈍角	介於90度到180度的角
平角	等於180度的角
優角	介於180度到360度的角
周角	等於360度的角

角的命名

1. 可以直接在角上面標示$1$、$2$、$3$、$4$、……，並稱呼為「$\angle 1$(讀作角$1$)」、「$\angle 2$」、「$\angle 3$」、「$\angle 4$」等等。
2. 在不會造成混淆的情況下，可以標示出頂點，並利用頂點命名。例如有一個角的頂點為$A$，我們稱此角為$\angle A$。
3. 若有可能造成混淆，可以在兩射線上各取一點，並以順時針或逆時針的方式報讀角的名字。如右圖為$\angle BAC$(順時針)或$\angle CAB$(逆時針)，但不可以稱$\angle ACB$或$\angle ABC$(即頂點必須在中間)。

• 下圖為一個可能會造成混淆的例子：

• 如果只是說$\angle A$，不知道是要表達$\angle BAC$、$\angle BAD$還是$\angle CAD$。
• 如果要表示最大的那個角，應該要用$\angle BAC$來說明比較好。

三角形

由三個點用線段互相連起來的圖形，我們稱為三角形。三角形具有$3$條邊、$3$個角與$3$個頂點。是中學時期學習最多的形狀。

• 依內角的大小可以將三角形區分成三類：

三角形種類	說明
銳角三角形	三個內角都是銳角
直角三角形	三個內角當中有一個直角
鈍角三角形	三個內角當中有一個鈍角

• 其中，依邊的長短可以分出特別的兩類三角形：

三角形種類	說明
等腰三角形	其中兩條邊等長
正三角形	三條邊都等長

三角形的命名

三角形的命名如同角的命名，可以順時針報讀或逆時針報讀，但它跟角報讀方式的不同之處在於三角形可以從任何點開始。如下圖，你可以稱下面這個三角形為$\triangle ABC$、$\triangle ACB$、$\triangle BAC$、$\triangle BCA$、$\triangle CAB$、$\triangle CBA$。
但在大部分的情形我們會習慣將英文字母按照順序排列，記作$\triangle ABC$，讀作「三角形$ABC$」，很少人稱作「$ABC$三角形」。

多邊形

由$3$個點以上(含)，相鄰的兩點以線段連成一圈的圖形，我們稱為多邊形。

• 一個$n$邊形有$n$個頂點、$n$條邊與$n$個角。
• 三角形也是一種多邊形。
• 國中階段會比較着墨在三角形、四邊形與正多邊形上。
• 多邊形的稱呼：從某一個頂點出發，依序以順時針或逆時針的順序報讀各頂點。一樣的，習慣上我們會按照英文字母的順序報讀。

此四邊形可以稱呼它為四邊形$ABCD$或四邊形$BADC$等等，但不能稱呼為四邊形$ACBD$。

• 多邊形的對角線：不相鄰的兩點連成的線，我們稱為對角線。

  

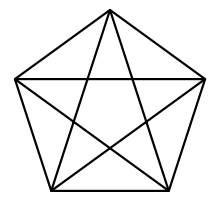
  圖中畫出五邊形所有的對角線。

  • 補充：$n$邊形的對角線有${\frac {n\times (n-3)}{2}}$個頂點。
• 若對角線全部都在圖形之內，我們稱此圖形為凸多邊形，若有一條對角線的部分會在圖形之外，則我們稱此圖形為凹多邊形。
  • 在國中數學內，沒有特別強調時，談論的圖形都是凸多邊形。

凸六邊形的例子。所有對角線(紅色線段)都在圖形內。

凹五邊形的例子。綠色的對角線有部分超出圖形之外。

圓

參見：國中數學/國中數學九年級/2-1 點、線、圓
在平面上，與一固定點$A$距離相同的所有點形成的圖形，我們稱為圓，其中「相同的距離」我們稱為半徑。

垂直

當兩直線(或線段)的夾角剛好是直角時，我們稱兩直線(或線段)垂直，並使用「$\bot$」表示。如下圖直線$l$與直線$g$垂直，我們可以寫作「$l\bot g$」。

垂線

垂線：一直線與直線$L$的夾角為直角(兩直線互相垂直)，則我們稱此直線為垂線。
1.一條直線$L$的垂線有無限多條。

• 如下圖當中，$L_{1}$、$L_{2}$與$L_{3}$都是$L$的垂線。
• 當然，只要在畫一條直線，其夾角與直線$L$成$90$度的時候，這條直線也會是直線$L$的垂線。

2.過$L$線上一點作$L$的垂線只有一條。

• 如上圖當中，過$A$點且與$L$垂直的直線只有$L_{1}$一條。

3.過$L$線外一點作$L$的垂線只有一條。

垂足

兩垂直的直線(或線段)所相交的點，我們稱為垂足。如上圖當中的$A$、$B$、$C$三點，分別是直線$L$與$L_{1}$、$L_{2}$、$L_{3}$的垂足。

平分

設一線段${\overline {AB}}$，若點$P$在${\overline {AB}}$上且滿足${\overline {PA}}={\overline {PB}}$，則我們稱$P$點平分${\overline {AB}}$，$P$點也稱作$A$、$B$兩點的中點。

垂直平分線

垂直平分線(中垂線)

若$P$點平分${\overline {AB}}$，則過$P$點且與${\overline {AB}}$垂直的直線我們稱為${\overline {AB}}$的垂直平分線，又稱作中垂線。

1. 只有線段才有垂直平分線，直線與射線沒有。
2. 一條線段的垂直平分線只有一條。

線對稱圖形

1. 線對稱圖形的意義：將一個平面圖形沿着某一條直線對摺，如果可以使直線兩側的圖形完全重疊，則此圖形為線對稱圖形。

   

   一些線對稱圖形，紅色直線為對稱軸。

   
   
2. 對稱軸：在線對稱圖形中，若沿着直線$L$對摺，直線$L$兩側的圖形完全重疊，則直線$L$稱為線對稱圖形的對稱軸。
   • 對應點：沿着對稱軸對摺，會剛好疊合的點。
   • 對應邊：沿着對稱軸對摺，會剛好疊合的邊。
   • 對應角：沿着對稱軸對摺，會剛好疊合的角。
   • 一個圖形的對稱軸可能不只一條。

     

     虛線為對稱軸。可以注意左上方的正方形有4條對稱軸。

     所以要表達對應點、對應邊或對應角時，應該要說明「以哪條直線為對稱軸，什麼的對應什麼是什麼」。
     • 例如：如下圖，以直線$L$為對稱軸，點$B$的對應點為點$G$，${\overline {FG}}$的對應邊為${\overline {BC}}$，$\angle CDE$的對應角為$\angle FED$。

以直線L為對稱軸的箭頭

• 註解：
  1. 在線對稱圖形中，對稱軸為兩側對稱點連線的垂直平分線。
     • 如上圖當中，直線$L$為${\overline {DE}}$的垂直平分線。
  2. 在線對稱圖形中，對稱線段等長，對稱角等大。
     • 如上圖當中${\overline {FG}}$的對應邊為${\overline {BC}}$，所以${\overline {FG}}={\overline {BC}}$、$\angle ABC$的對應角為$\angle AGF$，所以$\angle ABC=\angle AGF$。

常見的線對稱圖形

1. 等腰三角形
   • 等腰三角形的定義：有兩條邊相等的三角形。
   • 一般的等腰三角形只有一條對稱軸，此對稱軸既是底邊的垂直平分線，也會將頂角平分成兩個角度相等的角(我們稱作角平分線)。
   • 等腰三角形的兩個底角相等。
2. 正三角形
   • 正三角形必定有$3$條對稱軸。
   • 正三角形必然是等腰三角形，但等腰三角形不一定是正三角形。
3. 長方形
   • 長方形的定義：有四個直角的四邊形。
   • 一般的長方形有$2$條對稱軸。
4. 菱形
   • 菱形的定義：有四邊等長的四邊形。
   • 一般的菱形有$2$條對稱軸。
5. 正方形
   • 正方形的定義：四邊等長、四個角都是直角的四邊形。
   • 正方形必定有$4$條對稱軸。
   • 正方形必然是長方形，但長方形不一定是正方形。
   • 正方形必然是菱形，但菱形不一定是正方形。
6. 箏形
   • 箏形的定義：有兩對鄰邊相等的四邊形。
   • 箏形又稱作鳶形。
   • 一般的箏形只有一條對稱軸。
   • 正方形、菱形必然是箏形，但箏形不一定是正方形或菱形。
7. 等腰梯形
   • 等腰梯形的意義：一個梯形的兩腰等長。
   • 等腰梯形只有一條對稱軸。
8. 正多邊形
   • 正多邊形的對稱軸和它的邊數一樣多。如正七邊形有七條對稱軸。
9. 圓形
   • 圓形有無限多條對稱軸，任何一條直徑都是其對稱軸。

常考的"非"線對稱圖形

1. 內角分別是$30-60-90$度的三角形。
2. 一般的平行四邊形。
3. 一般的梯形。

剪紙與線對稱圖形

將一張紙對摺，並在摺線畫圖案，剪下來的圖形必定以摺線作為其對稱軸。

方格紙與線對稱圖形

其秘訣為：對稱點與對稱軸的距離相等，利用方格紙上的格子可以測量距離，找出對稱點然後再相連即可。