- 将 (1+1) 从一次方乘到四次
- 将 (x+1) 从一次方乘到四次
- 将 (a+b) 从一次方乘到四次
- 多项式
- 项
- 系数
- 次
- 元
- 杨辉三角形:
 展开的系数
展开的系数 
设  ,则函数
,则函数  在
在  点切线斜率、微分、导数、
点切线斜率、微分、导数、 、
、 、
、 、
、 、
、 都代表同一个意思。
都代表同一个意思。
y=ƒ(x):
- 单项式的 ƒ'(x)


- axn 对 x 的微分为 anxn-1 ,请证明
- n 为 0 (即常数),则微分为 0。因为微分代表“变化”,常数没有变化。
- 除 0 之外,n 不管是正数或负数、整数或非整数都成立,
- 多项式的 ƒ'(x)
- 每个单项皆微分
- 常数项微分为 0
- 微分之应用问题
- 更多例题
- 极限存在,它的左右极限存在且相等。
- 函数在一点可导的条件是:函数在该点的左右两侧导数都存在且相等。
- dy=ƒ'(x) dx 即 ƒ'(x) 曲线与
 轴所夹的微小面积。
轴所夹的微小面积。
- 原函数 ƒ(x)=0 时,x 值称为方程式的根。此处为函数图形与
 轴之交点。
轴之交点。
- 函数 ƒ(x) 与其导数函数 ƒ'(x) 的关系:
- 函数的转弯处 → 斜率为 0,ƒ'(x) 为 0 处,ƒ(x) 有极大值或极小值,斜率由正转负时有极大值,斜率由负转正时有极小值。
- 一系列的函数 ƒ(x) + C ,有相同的导函数 ƒ'(x) 。
适用所有可微分的方程式。
| 法则 | 表示式 | 简记 | 口诀 |
|---|
| 常数微分 |  | 常数'=0 | 常数微分为零 |
|---|
| 常系数微分 |  | (Cƒ(x))'=Cƒ'(x) | 常系数可提出 |
|---|
| 乘积法则 |  | (fg)'=f'g+fg' | 前导后不导
+前不导后导 |
|---|
| 链式法则 |  或 或  |  | 分子分母同乘d(g(x)) |
|---|
- 零次:
 ,
,
- 一次:
 ,
,
- 二次:
 ,
, ,更多抛物线图形
,更多抛物线图形
- 三次:
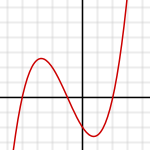 ,
,
- 四次:
 ,
,
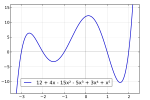
- 五次:
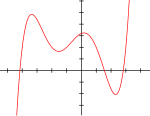 ,
,
由乘法公式  ,可以对任意一元二次方程式
,可以对任意一元二次方程式  进行配方,而以上的公式解也是由配方法推导出来的,推导过程如下:
进行配方,而以上的公式解也是由配方法推导出来的,推导过程如下:
![{\displaystyle {\begin{aligned}y&=f(x)\\\\&=ax^{2}+bx+c\\\\&=a\left(x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}\right)\\\\&=a\left[x^{2}+2\left({\frac {b}{2a}}\right)x+{\frac {c}{a}}\right]\\\\&=a\left[x^{2}+2\left({\frac {b}{2a}}\right)x+\left({\frac {b}{2a}}\right)^{2}-\left({\frac {b}{2a}}\right)^{2}+{\frac {c}{a}}\right]\\\\&=a\left[\left(x+{\frac {b}{2a}}\right)^{2}-\left({\frac {b}{2a}}\right)^{2}+{\frac {4ac}{4a^{2}}}\right]\\\\&=a\left[\left(x+{\frac {b}{2a}}\right)^{2}+{\frac {4ac-b^{2}}{4a^{2}}}\right]\\\\&=a\left(x+{\frac {b}{2a}}\right)^{2}+\left(c-{\frac {b^{2}}{4a}}\right)\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f78c8748887a9869fcbe86885e98b8f17dd2e58)
 时右侧斜向上,抛物线开口向上
时右侧斜向上,抛物线开口向上 ,有极小值
,有极小值 时右侧斜向下,抛物线开口向下
时右侧斜向下,抛物线开口向下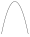 ,有极大值
,有极大值 或
或  时有极大值或极小值
时有极大值或极小值 
 (即图形交
(即图形交  )时为两根
)时为两根







设一元二次方程式  的解为
的解为  和
和  ,则有以下关系式:
,则有以下关系式:


这两个公式由设  和
和  为符合一元二次方程式公式解的写法来求出。
为符合一元二次方程式公式解的写法来求出。




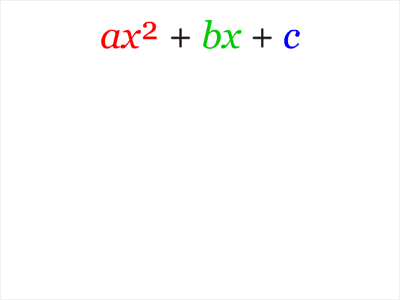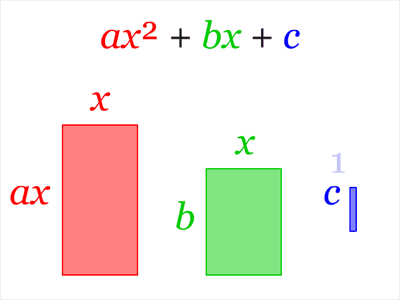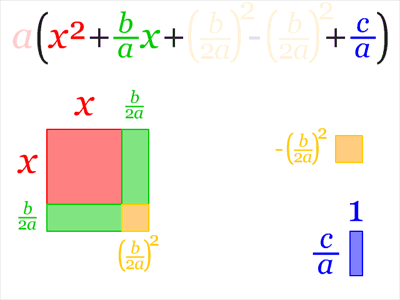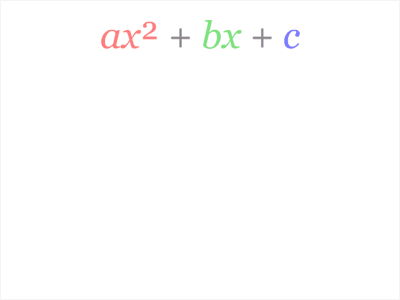
| 令 a=1,C=-c
 |
|---|
 ,
,
 ,
,
 ,
, ,更多抛物线图形
,更多抛物线图形 ,
,
 ,
,
 ,
,
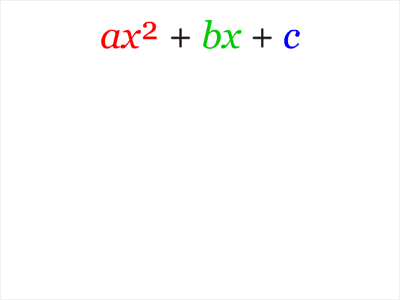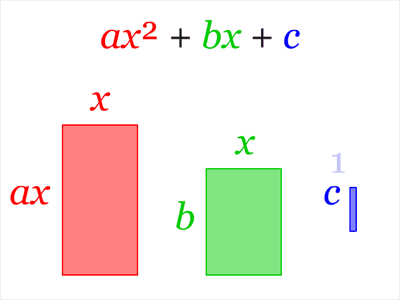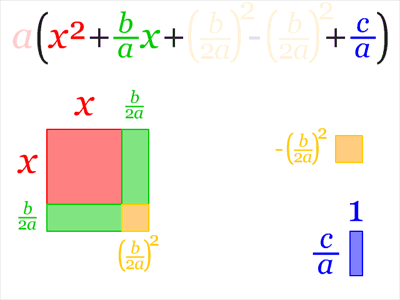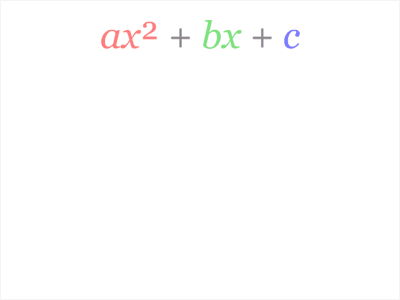





































![{\displaystyle {\begin{aligned}y&=f(x)\\\\&=ax^{2}+bx+c\\\\&=a\left(x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}\right)\\\\&=a\left[x^{2}+2\left({\frac {b}{2a}}\right)x+{\frac {c}{a}}\right]\\\\&=a\left[x^{2}+2\left({\frac {b}{2a}}\right)x+\left({\frac {b}{2a}}\right)^{2}-\left({\frac {b}{2a}}\right)^{2}+{\frac {c}{a}}\right]\\\\&=a\left[\left(x+{\frac {b}{2a}}\right)^{2}-\left({\frac {b}{2a}}\right)^{2}+{\frac {4ac}{4a^{2}}}\right]\\\\&=a\left[\left(x+{\frac {b}{2a}}\right)^{2}+{\frac {4ac-b^{2}}{4a^{2}}}\right]\\\\&=a\left(x+{\frac {b}{2a}}\right)^{2}+\left(c-{\frac {b^{2}}{4a}}\right)\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f78c8748887a9869fcbe86885e98b8f17dd2e58)


































