设函数 在点
在点 的某个邻域内有定义,当自变量
的某个邻域内有定义,当自变量 在
在 处取得增量
处取得增量 (点
(点 仍在该邻域内)时,相应地函数
仍在该邻域内)时,相应地函数 取得增量
取得增量 ;如果
;如果
 与
与
 之比当
之比当
 时的极限存在,则称函数
时的极限存在,则称函数 在点
在点 处可导,并称这个极限为函数
处可导,并称这个极限为函数 在点
在点 处的导数,记为
处的导数,记为 ,即
,即
 ,
,
也可记作 ,
, 或
或 
若将一点扩展成函数 在其定义域包含的某开区间
在其定义域包含的某开区间 内每一个点,那么函数
内每一个点,那么函数 在开区间
在开区间 内可导,这时对于
内可导,这时对于 内每一个确定的
内每一个确定的 值,都对应着
值,都对应着 的一个确定的导数,如此一来每一个导数就构成了一个新的函数,这个函数称作原函数
的一个确定的导数,如此一来每一个导数就构成了一个新的函数,这个函数称作原函数 的导函数,记作:
的导函数,记作: 、
、 或者
或者
导函数的定义表达式为:

值得注意的是,导数是一个数,是指函数 在点
在点 处导函数的函数值。但通常也可以说导函数为导数,其区别仅在于一个点还是连续的点。
处导函数的函数值。但通常也可以说导函数为导数,其区别仅在于一个点还是连续的点。
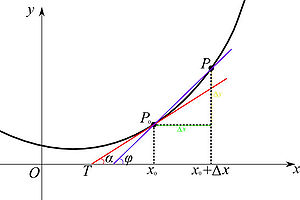
如右图所示,设 为曲线上的一个定点,
为曲线上的一个定点, 为曲线上的一个动点。当
为曲线上的一个动点。当 沿曲线逐渐趋向于点
沿曲线逐渐趋向于点 时,并且割线
时,并且割线 的极限位置
的极限位置 存在,则称
存在,则称 为曲线在
为曲线在 处的切线。
处的切线。
若曲线为一函数 的图像,那么割线
的图像,那么割线 的斜率为:
的斜率为:

当 处的切线
处的切线 ,即
,即 的极限位置存在时,此时
的极限位置存在时,此时 ,
, ,则
,则 的斜率
的斜率 为:
为:

上式与一般定义中的导数定义是完全相同,则 ,故导数的几何意义即曲线
,故导数的几何意义即曲线 在点
在点 处切线的斜率。
处切线的斜率。
如果一个函数的定义域为全体实数,即函数在 上都有定义,那么该函数是不是在定义域上处处可导呢?答案是否定的。函数在定义域中一点可导需要一定的条件是:函数在该点的左右两侧导数都存在且相等。这实际上是按照极限存在的一个充要条件(极限存在,它的左右极限存在且相等)推导而来:
上都有定义,那么该函数是不是在定义域上处处可导呢?答案是否定的。函数在定义域中一点可导需要一定的条件是:函数在该点的左右两侧导数都存在且相等。这实际上是按照极限存在的一个充要条件(极限存在,它的左右极限存在且相等)推导而来:

上式中,后两个式子可以定义为函数在 处的左右导数:
处的左右导数:
左导数:
|
右导数:
|
用两个函数的例子来说明函数可导的条件。
 sgn函数,符号函数
sgn函数,符号函数
1.上面这个符号函数在 处可导吗?
处可导吗?
 绝对值函数
绝对值函数
2.上面这个绝对值函数在 处可导吗?
处可导吗?
以上两个函数都是在定义域内连续的函数,由此就可以得出一个结论:连续的函数不一定处处可导。
但处处可导的函数一定处处连续。
在解决函数的导数问题上,利用定义是在过于麻烦。故利用定义来引申出几个基本的求导法则,以利于更好地解决各类求导的问题。
| 求导法则
|
| 1 |
![{\displaystyle [u(x)\pm v(x)]'=u'(x)\pm v'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/378f6458e2bf91f15106bdfe6f48d70d1c0664c3)
|
| 2 |
![{\displaystyle [u(x)v(x)]'=u'(x)v(x)+u(x)v'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/faff524404c03e591f2d52a13cbaa03b9e5a7a4d)
|
| 3 |
![{\displaystyle \left[{\frac {u(x)}{v(x)}}\right]'={\frac {u'(x)v(x)-u(x)v'(x)}{v^{2}(x)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8396395d5abe8b90bc675bb7b51a698a2aea8427)
|
特别地,对于常数 :
:
| 4 |
![{\displaystyle [Cv(x)]'=Cv'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae98b1aa1554066c593aea096f74f01e0a18bb23)
|
| 5 |
![{\displaystyle \left[{\frac {C}{v(x)}}\right]'={\frac {-Cv'(x)}{v^{2}(x)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5796ebcad97dc8925e999c75859dd87041c31a12)
|
以上法则的证明中,对于1,可以利用极限的运算法则验证;对于2,可以直接使用导数定义证明,证明如下:
- 证明
![{\displaystyle [u(x)v(x)]'=u'(x)v(x)+u(x)v'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/faff524404c03e591f2d52a13cbaa03b9e5a7a4d)
| 求导法则
|
| 1 |
![{\displaystyle \{u[v(x)]\}'=u'[v(x)]v'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f63a317774ce42ca6fce28410aa1c61e51a5039)
|
- 设函数
 在
在 的某个邻域内连续,严格单调,且在
的某个邻域内连续,严格单调,且在 可导而且
可导而且 成立。则它的反函数
成立。则它的反函数 在
在 可导,且有:
可导,且有:
![{\displaystyle [f^{-1}(y)]'={\frac {1}{f'(x)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37de5a97f5c8a1470410e50ad265bf30d12383da) 或者
或者
我们可以用一个例子来说明:试求函数 的导函数。
的导函数。
解:
 是
是 的反函数,且
的反函数,且 在
在 开区间上严格单调、可导,且
开区间上严格单调、可导,且 因此由反函数求导法则可得:在对应区间
因此由反函数求导法则可得:在对应区间 内有:
内有:

对于参数方程:
 ,其中
,其中 和
和 可导,且
可导,且 严格单调(?),
严格单调(?), ,根据复合函数求导法则和反函数求导法则可得参数方程的导数为:
,根据复合函数求导法则和反函数求导法则可得参数方程的导数为:

对于极坐标方程 ,根据参数方程的求导法则可得极坐标方程的导数为:
,根据参数方程的求导法则可得极坐标方程的导数为:
![{\displaystyle {\frac {dy}{dx}}={\frac {\left[\rho (\theta )\sin \theta \right]'}{\left[\rho (\theta )\cos \theta \right]'}}={\frac {\rho _{\theta }^{'}\sin \theta +\rho \cos \theta }{\rho _{\theta }^{'}\cos \theta -\rho \sin \theta }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6ea0ffe7c60556cc192b24035b628d0116b78f5)
隐函数的求导方法的基本思想是要把方程 中的看作
中的看作 的函数
的函数 ,方程两端对
,方程两端对 求导,然后再解出隐函数的导数
求导,然后再解出隐函数的导数 。
。
- 给出一个例子来进一步说明:
- 试求由方程
 所确定的
所确定的 关于
关于 的隐函数的导数
的隐函数的导数 ,其中
,其中 。
。
- 解:
- 方程的两边同时对
 求导得:
求导得:



- 通过例题,应当注意方程两边求导的对象是
 ,而
,而 是用
是用 表示的,相当于一个
表示的,相当于一个 的复合函数,故根据复合函数的求导法则:
的复合函数,故根据复合函数的求导法则:![{\displaystyle [f(y)]'=f'(y)\cdot y_{x}^{'}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d857aaf73e3ba0b70e2cc8b3f6ac686de6dfa452) 。本题中
。本题中
参数方程的高阶求导
对于参数方程:
 ,其中
,其中 和
和 二阶可导,且
二阶可导,且 ,则由
,则由 ,有
,有




![{\displaystyle ={\frac {\phi ''(t)\psi '(t)-\phi '(t)\psi ''(t)}{{[\psi '(t)]}^{2}}}\cdot {\frac {1}{\psi '(t)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dce117f6eafed655bb537a03ae8749e4308eb1d)
| 基本导数公式
|
| 1 |

|
| 2 |

|
| 3 |

|
| 4 |

|
| 5 |

|
| 6 |

|
| 7 |

|
| 8 |

|
| 9 |

|
| 10 |

|
| 11 |

|
| 12 |
 其中 其中
|
| 13 |

|
| 14 |

|
| 15 |

|
| 16 |

|
物理学、几何学、经济学等学科中的一些重要概念都可以用导数来表示。例如,在物理学中,速度被定义为位置函数的导数,即: ;而加速度被定义为速度函数的导数,即:
;而加速度被定义为速度函数的导数,即: 。另外,导数还可以表示曲线在一点的斜率,以及经济学中的边际和弹性。
。另外,导数还可以表示曲线在一点的斜率,以及经济学中的边际和弹性。

















































![{\displaystyle [u(x)\pm v(x)]'=u'(x)\pm v'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/378f6458e2bf91f15106bdfe6f48d70d1c0664c3)
![{\displaystyle [u(x)v(x)]'=u'(x)v(x)+u(x)v'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/faff524404c03e591f2d52a13cbaa03b9e5a7a4d)
![{\displaystyle \left[{\frac {u(x)}{v(x)}}\right]'={\frac {u'(x)v(x)-u(x)v'(x)}{v^{2}(x)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8396395d5abe8b90bc675bb7b51a698a2aea8427)

![{\displaystyle [Cv(x)]'=Cv'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae98b1aa1554066c593aea096f74f01e0a18bb23)
![{\displaystyle \left[{\frac {C}{v(x)}}\right]'={\frac {-Cv'(x)}{v^{2}(x)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5796ebcad97dc8925e999c75859dd87041c31a12)
![{\displaystyle [u(x)v(x)]'=\lim _{\Delta x\to 0}{\frac {u(x+\Delta x)v(x+\Delta x)-u(x)v(x)}{\Delta x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42842262ea75b964bf3cac0750f722ac734179cd)
![{\displaystyle =\lim _{\Delta x\to 0}\left[{\frac {u(x+\Delta x)-u(x)}{\Delta x}}\cdot v(x+\Delta x)+u(x)\cdot {\frac {v(x+\Delta x)-v(x)}{\Delta x}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14410afc9e91a14be7b8a0ff6a692d85e23fb5b4)



![{\displaystyle \{u[v(x)]\}'=u'[v(x)]v'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f63a317774ce42ca6fce28410aa1c61e51a5039)




![{\displaystyle [f^{-1}(y)]'={\frac {1}{f'(x)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37de5a97f5c8a1470410e50ad265bf30d12383da)















![{\displaystyle {\frac {dy}{dx}}={\frac {\left[\rho (\theta )\sin \theta \right]'}{\left[\rho (\theta )\cos \theta \right]'}}={\frac {\rho _{\theta }^{'}\sin \theta +\rho \cos \theta }{\rho _{\theta }^{'}\cos \theta -\rho \sin \theta }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6ea0ffe7c60556cc192b24035b628d0116b78f5)








![{\displaystyle [f(y)]'=f'(y)\cdot y_{x}^{'}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d857aaf73e3ba0b70e2cc8b3f6ac686de6dfa452)







![{\displaystyle ={\frac {\phi ''(t)\psi '(t)-\phi '(t)\psi ''(t)}{{[\psi '(t)]}^{2}}}\cdot {\frac {1}{\psi '(t)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dce117f6eafed655bb537a03ae8749e4308eb1d)



















